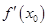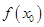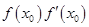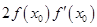题目内容
已知函数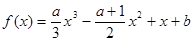 ,其中
,其中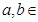 R.
R.
(1)若曲线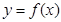 在点
在点 处的切线方程为
处的切线方程为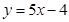 ,求函数
,求函数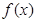 的解析
的解析
式;
(2)当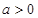 时,讨论函数
时,讨论函数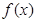 的单调性.
的单调性.
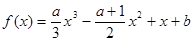 ,其中
,其中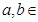 R.
R.(1)若曲线
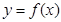 在点
在点 处的切线方程为
处的切线方程为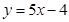 ,求函数
,求函数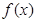 的解析
的解析式;
(2)当
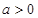 时,讨论函数
时,讨论函数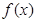 的单调性.
的单调性.(1) (2)见解析
(2)见解析
 (2)见解析
(2)见解析本试题主要是考查了导数的几何意义的运用,以及运用导数的正负判定函数单调性的综合运用。
(1) ,……2分 由导数的几何意义得
,……2分 由导数的几何意义得 ,
,
于是 由切点
由切点 在直线
在直线 上可知
上可知 ,得到b的值,进而得到解析式。
,得到b的值,进而得到解析式。
(2)因为 ,然后对于参数a进行分类讨论得到参数的取值范围求解得到。解:(1)
,然后对于参数a进行分类讨论得到参数的取值范围求解得到。解:(1) ,……2分 由导数的几何意义得
,……2分 由导数的几何意义得 ,
,
于是 .….3分 由切点
.….3分 由切点 在直线
在直线 上可知
上可知 ,
,
解得 所以函数
所以函数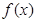 的解析式为
的解析式为 . …5分
. …5分
(2) , ……6分
, ……6分
当 时,
时, ,函数
,函数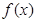 在区间
在区间 及
及 上为增函数;
上为增函数;
在区间 上为减函数; .……8分
上为减函数; .……8分
当 时,
时, ,函数
,函数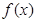 在区间
在区间 上为增函数;…….…10分
上为增函数;…….…10分
当 时,
时, ,函数
,函数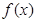 在区间
在区间 及
及 上为增函数;
上为增函数;
在区间 上为减函数. .……12分
上为减函数. .……12分
(1)
 ,……2分 由导数的几何意义得
,……2分 由导数的几何意义得 ,
,于是
 由切点
由切点 在直线
在直线 上可知
上可知 ,得到b的值,进而得到解析式。
,得到b的值,进而得到解析式。(2)因为
 ,然后对于参数a进行分类讨论得到参数的取值范围求解得到。解:(1)
,然后对于参数a进行分类讨论得到参数的取值范围求解得到。解:(1) ,……2分 由导数的几何意义得
,……2分 由导数的几何意义得 ,
,于是
 .….3分 由切点
.….3分 由切点 在直线
在直线 上可知
上可知 ,
,解得
 所以函数
所以函数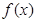 的解析式为
的解析式为 . …5分
. …5分(2)
 , ……6分
, ……6分当
 时,
时, ,函数
,函数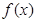 在区间
在区间 及
及 上为增函数;
上为增函数;在区间
 上为减函数; .……8分
上为减函数; .……8分当
 时,
时, ,函数
,函数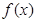 在区间
在区间 上为增函数;…….…10分
上为增函数;…….…10分当
 时,
时, ,函数
,函数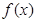 在区间
在区间 及
及 上为增函数;
上为增函数;在区间
 上为减函数. .……12分
上为减函数. .……12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
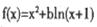 ,其中
,其中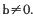
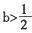 时,判断函数
时,判断函数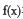 在定义域上的单调性;
在定义域上的单调性;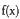 的极值点;
的极值点;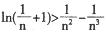 都成立.
都成立.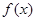 的图象在点P处的切线方程是y=-x+8,则f(5)+f’(5)=
的图象在点P处的切线方程是y=-x+8,则f(5)+f’(5)=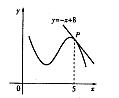
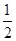
 是曲线
是曲线 在
在 处的切线,
处的切线, ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )



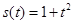 ,则运动开始后4s时物体的动能是( )(其中
,则运动开始后4s时物体的动能是( )(其中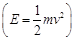 ).
).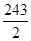 J
J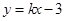 与曲线
与曲线 相切,则实数
相切,则实数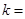 .
.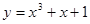 在点(1,3)处的切线方程是( )
在点(1,3)处的切线方程是( )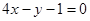
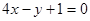
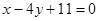
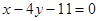
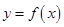 在
在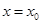 处可导,则
处可导,则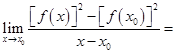 ( )
( )