题目内容
设数列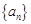 的前
的前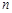 项和为
项和为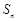 ,且满足
,且满足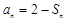
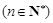 .
.
(1)求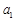 ,
, ,
,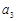 ,
,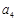 的值并写出其通项公式;(2)证明数列
的值并写出其通项公式;(2)证明数列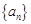 是等比数列.
是等比数列.
(Ⅰ) ;
; ;
; ;
; 。
。 ;(2)详见解析
;(2)详见解析
解析试题分析:(1)由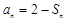 ,得
,得 ;
; ;
; ;
; ,故可猜想
,故可猜想 。(2)根据已知
。(2)根据已知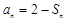 和
和 可推导出
可推导出 。根据等比数列的定义可知,数列
。根据等比数列的定义可知,数列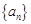 是首项为1公比为2的等比数列。
是首项为1公比为2的等比数列。
解:(1)由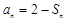 ,得
,得 ;
; ;
; ;
; ,
,
猜想
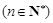 . 6分
. 6分
(2)方法一: ①
①  ②
②
②-①得  ∴
∴ 即
即
∴数列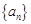 是等比数列. 13分
是等比数列. 13分
方法二:(三段论)∵通项公式为 的数列
的数列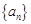 ,若
,若 ,
, 是非零常数,则
是非零常数,则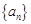 是等比数列;
是等比数列;
由(1)通项公式 ,即
,即 ;∴通项公式
;∴通项公式 的数列
的数列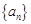 是等比数列.
是等比数列.
考点:1 与
与 的关系;2等比数列的定义。
的关系;2等比数列的定义。

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 ,则a5= .
,则a5= . ,则
,则 =_________.
=_________. 满足:
满足: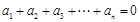 且
且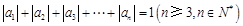 ,则称数列
,则称数列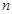 阶“归化数列”.
阶“归化数列”.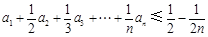 .
.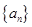 为等差数列,且
为等差数列,且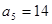 ,
,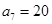 ,数列
,数列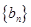 的前
的前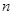 项和为
项和为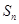 ,
,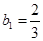 且
且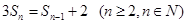 .
.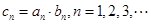 ,
,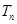 为数列
为数列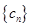 的前
的前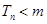 对
对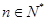 恒成立,求
恒成立,求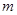 的最小值.
的最小值.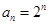 ,把数列
,把数列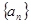 的各项排成如图所示的三角形状,记
的各项排成如图所示的三角形状,记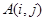 表示第i行中第j个数,则结论
表示第i行中第j个数,则结论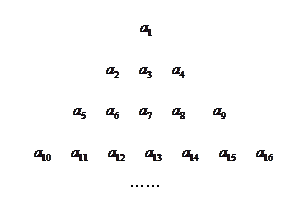
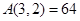 ;
;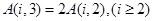 ;
;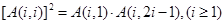 ;
;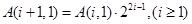 .
. 、
、 、
、 成等比数列,那么公比为( )
成等比数列,那么公比为( )


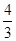
 中,有
中,有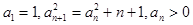 ,则通项
,则通项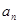 = .
= .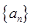 ,对任意的
,对任意的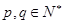 满足
满足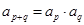 ,且
,且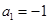 ,那么
,那么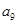 等于
等于