题目内容
下列函数中,在其定义域内,既是单调递增函数,又是奇函数的是( )
| A.f(x)=sinx+x2 | B.f(x)=
| C.f(x)=lnx-
| D.f(x)=3x-3-x |
根据函数奇偶性的定义可得:若函数具有奇偶性则其定义域关于原点对称,因为函数f(x)=lnx-
的定义域为(0,+∞),所以此函数不具有奇偶性,所以C答案错误.
A:因为函数的解析式为f(x)=sinx+x2,所以f(-x)≠-f(x),所以此函数在定义域内不是奇函数,所以A错误.
B:由函数f(x)=
+x可得:f′(x)=1-
,所以f′(x)=1-
≥0在其定义域内不是恒成立,所以函数在定义域内不是单调递增函数,所以B错误.
D:由函数f(x)=3x-3-x可得f(-x)=-f(x),并且f′(x)=3xln3+
>0恒成立,所以此函数既是单调递增函数,又是奇函数,所以D正确.
故选D.
| 1 |
| x |
A:因为函数的解析式为f(x)=sinx+x2,所以f(-x)≠-f(x),所以此函数在定义域内不是奇函数,所以A错误.
B:由函数f(x)=
| 1 |
| x3 |
| 3 |
| x4 |
| 3 |
| x4 |
D:由函数f(x)=3x-3-x可得f(-x)=-f(x),并且f′(x)=3xln3+
| ln3 |
| 3x |
故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
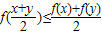 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数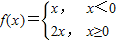
 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数