题目内容
已知椭圆
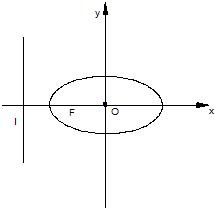
+y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.求三棱锥A-F1F2B的体积;
| x2 | 2 |

分析:利用椭圆的标准方程及其性质、面面垂直的性质及三棱锥的体积计算公式即可得出;
解答:(本小题满分13分)
解:依题意得:
+y2=1的顶点A(0,1),F1(-1,0),F2(1,0)
直线AF1:y=x+1,
联立方程组
⇒x2+2(x+1)2=2⇒3x2+4x=0,
x1=0,x2=-
∴B(-
,-
)∴S△F1BF2=
×|F1F2|×|yB|=
×2×
=
…(7分)
又∵面AF1F2⊥面BF1F2,而AO⊥F1F2,面AF1F2∩面BF1F2=F1F2,AO?面AF1F2
∴AO⊥面BF1F2,即AO为锥A-F1F2B的高,
故VA-F1FBB=
S△BF1F2×h=
×
×1=
…(13分)
解:依题意得:
| x2 |
| 2 |
直线AF1:y=x+1,
联立方程组
|
x1=0,x2=-
| 4 |
| 3 |
∴B(-
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
又∵面AF1F2⊥面BF1F2,而AO⊥F1F2,面AF1F2∩面BF1F2=F1F2,AO?面AF1F2
∴AO⊥面BF1F2,即AO为锥A-F1F2B的高,
故VA-F1FBB=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
点评:本题考查椭圆的标准方程及其性质、线面与面面垂直的判定和性质定理及三棱锥的体积计算公式、考查空间想象能力以及计算能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 已知椭圆
已知椭圆 已知椭圆
已知椭圆