题目内容
已知函数 ,其定义域为
,其定义域为 (
( ).
).
(Ⅰ)试确定 的取值范围,使得函数
的取值范围,使得函数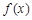 在
在 上为单调函数;
上为单调函数;
(Ⅱ)求证:对于任意的 ,总存在
,总存在 ,满足
,满足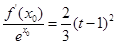 ,并确定这样的
,并确定这样的 的个数.
的个数.
【答案】
(Ⅰ)因为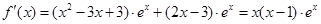 ……2分
……2分
由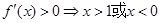 ;由
;由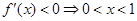 ,所以
,所以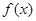 在
在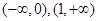 上递增,在
上递增,在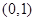 上递减……4分
上递减……4分
要使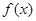 在
在 上为单调函数,则
上为单调函数,则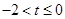 ……6分
……6分
(Ⅲ)证:因为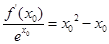 ,所以
,所以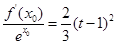 ,即为
,即为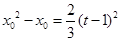 ,
,
令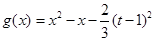 ,从而问题转化为证明方程
,从而问题转化为证明方程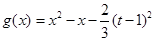 =0在
=0在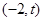 上有解,并讨论解的个数……8分
上有解,并讨论解的个数……8分
因为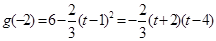 ,
,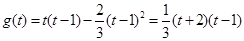 ,所以
,所以
①当 时,
时,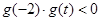 ,所以
,所以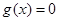 在
在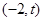 上有解,且只有一解
上有解,且只有一解
②当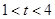 时,
时,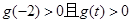 ,但由于
,但由于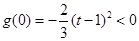 ,
,
所以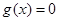 在
在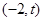 上有解,且有两解……10分
上有解,且有两解……10分
③当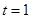 时,
时,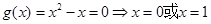 ,所以
,所以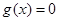 在
在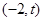 上有且只有一解;
上有且只有一解;
当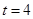 时,
时,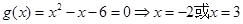 ,
,
所以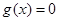 在
在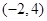 上也有且只有一解……12分
上也有且只有一解……12分
综上所述, 对于任意的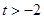 ,总存在
,总存在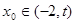 ,满足
,满足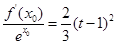 ,
,
且当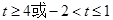 时,有唯一的
时,有唯一的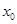 适合题意;当
适合题意;当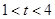 时,有两个
时,有两个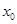 适合题意
适合题意
【解析】略

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,其定义域为
,其定义域为 (
( ),设
),设 .
. 的取值范围,使得函数
的取值范围,使得函数 在
在 的大小并说明理由;
的大小并说明理由; ,满足
,满足 ,并确定这样的
,并确定这样的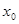 的个数.
的个数. ,其定义域为
,其定义域为 (
(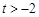 ),设
),设 。
。 的取值范围,使得函数
的取值范围,使得函数 在
在 的大小并说明理由;
的大小并说明理由; ,满足
,满足 ,并确定这样的
,并确定这样的 的个数。
的个数。