题目内容
18.z1=1-2i,z2=3+4i,z3=2+i,$w={z_1}^2$+$\overline{z_2}-\frac{i}{z_3}$,求复数w.分析 由题意、共轭复数和复数代数形式的加减乘除运算,依次求出${{z}_{1}}^{2}$、$\overline{{z}_{2}}、\frac{i}{{z}_{3}}$,代入w整理出实部和虚部即可.
解答 解:∵z1=1-2i,z2=3+4i,z3=2+i,
∴${z_1}^2=(1-2i{)^2}=-3-4i$,$\overline{z_2}$=3-4i,$\frac{i}{z_3}=\frac{i}{2+i}=\frac{-1+2i}{5}$,…(6分)
∴$w={z_1}^2$+$\overline{z_2}-\frac{i}{z_3}$=-3-4i+3-4i-$\frac{-1+2i}{5}$=$\frac{1}{5}-\frac{42}{5}i$.…(12分)
点评 本题考查共轭复数的定义,复数代数形式的加减乘除运算,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
9.命题“对于任意的x∈R,x2+1>0”的否定是( )
| A. | 对于任意的x∈R,x2+1≤0 | B. | 存在x∈R,x2+1≤0 | ||
| C. | 存在x∈R,x2+1<0 | D. | 存在x∈R,x2+1>0 |
13.已知二次函数f(x)=ax2+bx-3在x=1处取得极值,且在(0,-3)点处的切线与直线2x+y=0平行.
(1)求f(x)的解析式;
(2)求函数g(x)=xf(x)+4x的单调递增区间及极值.
(1)求f(x)的解析式;
(2)求函数g(x)=xf(x)+4x的单调递增区间及极值.
10.已知直线l经过点P(3,4).
(1)若直线l的倾斜角为θ(θ≠90°),且直线l经过另外一点(cosθ,sinθ),求此时直线的方程;
(2)若直线l与两坐标轴围成等腰直角三角形,求直线l的方程.
(1)若直线l的倾斜角为θ(θ≠90°),且直线l经过另外一点(cosθ,sinθ),求此时直线的方程;
(2)若直线l与两坐标轴围成等腰直角三角形,求直线l的方程.
7.下列有关命题说法正确的是( )
| A. | 命题“若x2=4,则x=2”的否命题为“若x2=4,则x≠2” | |
| B. | 所有常数列既是等差数列也是等比数列 | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为假命题 | |
| D. | 命题“?x∈R,x2+x<0”的否定是“?x∈R,x2+x≥0”. |
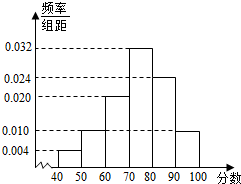 某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.