题目内容
已知向量
(1)若 ,求tanx的值;
,求tanx的值;
(2)若 ,又x为第三象限角,求sinx+cosx的值.
,又x为第三象限角,求sinx+cosx的值.
解:(1)∵ ,又
,又 ,
,
可得sinx+2cosx=0,解得tanx=-2;
(2)∵ ,∴
,∴ ,即2sinxcosx-1=0,解得2sinxcosx=1,
,即2sinxcosx-1=0,解得2sinxcosx=1,
又(sinx+cosx)2=1+2sinxcosx=2,
∵x为第三象限角,∴sinx+cosx<0,
故sinx+cosx=-
分析:(1)由向量平行的充要条件可得sinx+2cosx=0,变形可得tanx的值;
(2)由向量垂直的充要条件可得2sinxcosx=1,而(sinx+cosx)2=1+2sinxcosx=2,结合x的象限可得sinx+cosx<0,开方可得答案.
点评:本题考查向量平行与垂直的充要条件,涉及三角函数的运算,属基础题.
 ,又
,又 ,
,可得sinx+2cosx=0,解得tanx=-2;
(2)∵
 ,∴
,∴ ,即2sinxcosx-1=0,解得2sinxcosx=1,
,即2sinxcosx-1=0,解得2sinxcosx=1,又(sinx+cosx)2=1+2sinxcosx=2,
∵x为第三象限角,∴sinx+cosx<0,
故sinx+cosx=-

分析:(1)由向量平行的充要条件可得sinx+2cosx=0,变形可得tanx的值;
(2)由向量垂直的充要条件可得2sinxcosx=1,而(sinx+cosx)2=1+2sinxcosx=2,结合x的象限可得sinx+cosx<0,开方可得答案.
点评:本题考查向量平行与垂直的充要条件,涉及三角函数的运算,属基础题.

练习册系列答案
相关题目

 ,求
,求 的值;
的值; ,
, 在
在 中,角A、B、C的对边分别是
中,角A、B、C的对边分别是 ,且满
,且满 ,求
,求 的取值范围。
的取值范围。
 ,求
,求 的值;
的值; ,
, 在
在 中,角A、B、C的对边分别是
中,角A、B、C的对边分别是 ,且满
,且满 ,求
,求 的取值范围。
的取值范围。
 ,求
,求 的值;
的值;
 求
求 的值。
的值。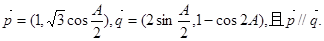
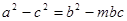 ,求实数m的值。
,求实数m的值。 ,求△ABC面积的最大值.
,求△ABC面积的最大值.