题目内容
已知数列{an}满足a1=
，an=
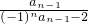（n≥2，n∈N*）．
（1）证明：数列{
+（-1）n}是等比数列．
（2）设bn=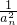
，求数列{bn}的前n项和Sn．
解：（Ⅰ）=（-1）n-
，∴+（-1）n=（-2）[
+（-1）n-1]
∴数列{+（-1）n}是以
+（-1）=3为首项，公比为-2的等比数列．
∴+（-1）n=3（-2）n-1，即an=
．
（Ⅱ）bn=（3×2n-1+1）2=9×4n-1+6×2n-1+1．
∴Sn=9×
+6×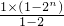
+n=3×4n+6×2n+n-9．
分析：（Ⅰ）由题设条件能够导出+（-1）n=（-2）[+（-1）n-1]，由此可知数列{+（-1）n}是以+（-1）=3为首项，公比为-2的等比数列．
（Ⅱ）bn=（3×2n-1+1）2=9×4n-1+6×2n-1+1．由此可求出数列{bn}的前n项和Sn．
点评：本题考查数列的递推公式和数列的求和，解题时要注意数列求和的方法总结和公式的合理运用．
=（-1）n-，∴+（-1）n=（-2）[+（-1）n-1]∴数列{
+（-1）n}是以+（-1）=3为首项，公比为-2的等比数列．∴
+（-1）n=3（-2）n-1，即an=．（Ⅱ）bn=（3×2n-1+1）2=9×4n-1+6×2n-1+1．
∴Sn=9×
+6×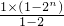+n=3×4n+6×2n+n-9．分析：（Ⅰ）由题设条件能够导出
+（-1）n=（-2）[+（-1）n-1]，由此可知数列{+（-1）n}是以+（-1）=3为首项，公比为-2的等比数列．（Ⅱ）bn=（3×2n-1+1）2=9×4n-1+6×2n-1+1．由此可求出数列{bn}的前n项和Sn．
点评：本题考查数列的递推公式和数列的求和，解题时要注意数列求和的方法总结和公式的合理运用．
练习册系列答案
相关题目