题目内容
已知函数f(x)=lnx+a(x+1).
(I)讨论函数f(x)的单调性;(II)求函数f(x)在[1,2]上的最大值.
解:(Ⅰ)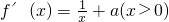 ,
,
(1)a≥0时,函数f(x)在(0,+∞)单调递增;
(2)a<0时,函数f(x)在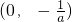 单调递增;
单调递增;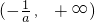 单调递减.(5分)
单调递减.(5分)
(Ⅱ)(1)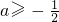 时,函数f(x)在[1,2]上单调递增,最大值为3a+ln2;
时,函数f(x)在[1,2]上单调递增,最大值为3a+ln2;
(2)a≤-1时,函数f(x)在[1,2]上单调递减,最大值为2a;
(3)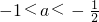 时,函数f(x)在
时,函数f(x)在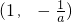 单调递增;
单调递增; 单调递减,最大值为
单调递减,最大值为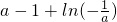 .(12分)
.(12分)
分析:(I)函数的定义域(0,+∞)分a≥0,a<0两种情况讨论f(x)在区间(0,+∞)上的单调性
(II)令f′(x)=0?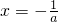 ,分①
,分①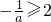 ;②
;②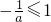 ;③
;③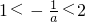 三种情况讨论函数在区间上的单调性,以确定函数的最大值.
三种情况讨论函数在区间上的单调性,以确定函数的最大值.
点评:本题主要考查了导数的应用:利用导数求函数的单调区间及求函数在闭区间[a,b]上的最值是通过比较函数在(a,b)内所有极值与端点函数值f(a),f(b) 比较而得到.要注意分类讨论思想在解题中的应用.
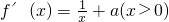 ,
,(1)a≥0时,函数f(x)在(0,+∞)单调递增;
(2)a<0时,函数f(x)在
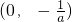 单调递增;
单调递增;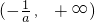 单调递减.(5分)
单调递减.(5分)(Ⅱ)(1)
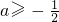 时,函数f(x)在[1,2]上单调递增,最大值为3a+ln2;
时,函数f(x)在[1,2]上单调递增,最大值为3a+ln2;(2)a≤-1时,函数f(x)在[1,2]上单调递减,最大值为2a;
(3)
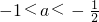 时,函数f(x)在
时,函数f(x)在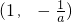 单调递增;
单调递增; 单调递减,最大值为
单调递减,最大值为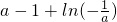 .(12分)
.(12分)分析:(I)函数的定义域(0,+∞)分a≥0,a<0两种情况讨论f(x)在区间(0,+∞)上的单调性
(II)令f′(x)=0?
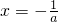 ,分①
,分①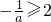 ;②
;②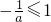 ;③
;③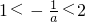 三种情况讨论函数在区间上的单调性,以确定函数的最大值.
三种情况讨论函数在区间上的单调性,以确定函数的最大值.点评:本题主要考查了导数的应用:利用导数求函数的单调区间及求函数在闭区间[a,b]上的最值是通过比较函数在(a,b)内所有极值与端点函数值f(a),f(b) 比较而得到.要注意分类讨论思想在解题中的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目