题目内容
以a、b、c依次表示方程2x+x=1、2x+x=2、3x+x=2的解,则a、b、c的大小关系为
a<c<b
a<c<b
.分析:因为a、b、c依次表示方程2x+x=1、2x+x=2、3x+x=2的解,所以把求方程的解转化为找两个函数图象交点的横坐标,在平面直角坐标系中作出对应的函数图象,则可直观地得到答案.
解答: 解:由2x+x=1、2x+x=2、3x+x=2,
解:由2x+x=1、2x+x=2、3x+x=2,
分别得:2x=1-x、2x=2-x、3x=2-x
所以a为函数y=2x与y=1-x的交点的横坐标,
b为函数y=2x与y=2-x的交点的横坐标,
c为y=3x与y=2-x的交点的横坐标.
由图象可知;a<c<b.
故答案为a<c<b.
 解:由2x+x=1、2x+x=2、3x+x=2,
解:由2x+x=1、2x+x=2、3x+x=2,分别得:2x=1-x、2x=2-x、3x=2-x
所以a为函数y=2x与y=1-x的交点的横坐标,
b为函数y=2x与y=2-x的交点的横坐标,
c为y=3x与y=2-x的交点的横坐标.
由图象可知;a<c<b.
故答案为a<c<b.
点评:本题考查了不等关系和不等式,考查了数形结合的解题思想,考查了转化思想,解答此题的关键是能够正确作出函数y=2x和y=3x的图象.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
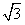 c,0)三点,其中c>0,
c,0)三点,其中c>0,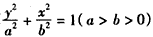 (其中a2-b2=c2)的左、右顶点分别为D,B,圆M与x轴的两个交点分别为A,C,且A点在B点右侧,C点在D点右侧,
(其中a2-b2=c2)的左、右顶点分别为D,B,圆M与x轴的两个交点分别为A,C,且A点在B点右侧,C点在D点右侧,