题目内容

已知a>0且a≠1，f（loga x）=（x-）.

（1）试证明函数y=f（x）的单调性.

（2）是否存在实数m满足：当y=f（x）的定义域为（-1，1）时，有f（1-m）+f（1-m2）＜0?若存在，求出其取值范围；若不存在，请说明理由.

（3）若函数f（x）-4恰好在（-∞，2）上取负值，求a的值.

（1）证明：由f（loga x）=（x-），得f（x）=（ax-a-x），x∈R，任取x1＜x2，f（x1）-f（x2）=（ -）.a>1时，，a2-1>0；0＜a＜1时，>，a2-1＜0.综上可得f（x1）＜f（x2），即函数为减函数.

（2）解：因为f（-x）=-（ax-a-x）=-f（x），即函数为奇函数，f（1-m）+f（1-m2）＜0可转化为f（1-m）＜f（m2-1），所以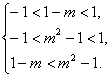解得

（3）解：f（x）-4恰好在（-∞，2）的值为负，即当x∈（-∞，2）时，有f（x）-4＜f（2）-4=0，解得a=2±.


练习册系列答案
相关题目
已知函数f（x）=ax+b，当x∈[a1，b1]时，f（x）的值域为[a2，b2]，当x∈[a2，b2]时，f（x）的值域为[a3，b3]，…当x∈[an-1，bn-1]时，f（x）的值域为[an，bn]，其中a，b为常数，a1=0，b1=1．
（Ⅰ）a=1时，求数列{an}与{bn}的通项；
（Ⅱ）设a＞0且a≠1，若数列{bn}是公比不为1的等比数列，求b的值；
（Ⅲ）若a＞0，设{an}与{bn}的前n项和分别记为Sn与Tn，求（T1+T1+…+Tn）-（S1+S2+…+Sn）的值．
（2013•松江区二模）已知双曲线C的中心在原点，D（1，0）是它的一个顶点，
d
=(1，
2
)是它的一条渐近线的一个方向向量．
（1）求双曲线C的方程；
（2）若过点（-3，0）任意作一条直线与双曲线C交于A，B两点 （A，B都不同于点D），求证：
DA
•
DB
为定值；
（3）对于双曲线Γ：
x2
a2
-
y2
b2
=1(a＞0，b＞0，a≠b)，E为它的右顶点，M，N为双曲线Γ上的两点（都不同于点E），且EM⊥EN，那么直线MN是否过定点？若是，请求出此定点的坐标；若不是，说明理由．然后在以下三个情形中选择一个，写出类似结论（不要求书写求解或证明过程）．
情形一：双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0，a≠b)及它的左顶点；
情形二：抛物线y2=2px（p＞0）及它的顶点；
情形三：椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)及它的顶点．
已知函数f(x)=
a
x
+x+(a-1)lnx+15a，F（x）=2x3-3（2a+3）x2+12（a+1）x+12a+2，其中a＜0且a≠-1．
（Ⅰ） 当a=-2，求函数f（x）的单调递增区间；
（Ⅱ） 若x=-1时，函数F（x）有极值，求函数F（x）图象的对称中心的坐标；
（Ⅲ）设函数g（x）=
F(x)，x≤1
f(x)，x＞1
（e是自然对数的底数），是否存在a使g（x）在[a，-a]上为减函数，若存在，求实数a的范围；若不存在，请说明理由．
22.已知集合M是满足下列性质的函数f（x）的全体：存在非零常数T，对任意x∈R,有f（x+T）=Tf（x）成立.

（1）函数f（x）=x是否属于集合M？说明理由；

（2）设函数f（x）=ax（a>0且a≠1）的图象与y=x的图象有公共点，证明：f（x）=ax∈M;

（3）若函数f（x）=sinkx∈M,求实数k的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网