题目内容
设动圆C与两圆C1：(x+
)2+y2=4，C2：(x-
)2+y2=4中的一个内切，另一个外切．则动圆C的圆心M轨迹L的方程是
-y2=1
-y2=1．
| 5 |
| 5 |
| x2 |
| 4 |
| x2 |
| 4 |
分析：由题意直接利用已知列出关系式，结合圆锥曲线的定义，即可求出圆心M的轨迹方程．
解答：解：根据题意，有
，或
∴|MC1|-|MC2|=4＜|C1C2|=2
，或|MC2|-|MC1|=4＜|C1C2|=2
所以，圆心M的轨迹是以C1、C2为焦点的双曲线，
故M的轨迹方程为：
-y2=1
故答案为：
-y2=1
|
|
∴|MC1|-|MC2|=4＜|C1C2|=2
| 5 |
| 5 |
所以，圆心M的轨迹是以C1、C2为焦点的双曲线，
故M的轨迹方程为：
| x2 |
| 4 |
故答案为：
| x2 |
| 4 |
点评：本题考查曲线轨迹方程的求法，圆的几何性质的应用和圆锥曲线的定义是解决问题的关键，属基础题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
)2＋y2＝4，C2：(x－
)2＋y2＝4中的一个内切，另一个外切．则动圆C的圆心M轨迹L的方程是________．
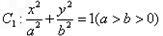的离心率为
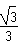，直线
:
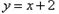与以原点为圆心、以椭圆C1的短半轴长为半径的圆相切.