题目内容
已知函数f(x)=3ax4-2(3a+1)x2+4x,
(Ⅰ)当a=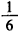 时,求f(x)的极值;
时,求f(x)的极值;
(Ⅱ)若f(x)在(-1,1)上是增函数,求a的取值范围.
(Ⅰ)当a=
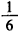 时,求f(x)的极值;
时,求f(x)的极值; (Ⅱ)若f(x)在(-1,1)上是增函数,求a的取值范围.
解:(Ⅰ)f′(x)=4(x-1)(3ax2+3ax-1),
当a=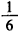 时,f′(x)=2(x+2)(x-1)2,
时,f′(x)=2(x+2)(x-1)2,
当x<-2时,f′(x)<0,当x>-2时,f′(x)>0,
∴f(x)在(-∞,-2)内单调减,在(-2,+∞)内单调增,
∴在x=-2时,f(x)有极小值,
所以,f(-2)=-12是f(x)的极小值.
(Ⅱ)在(-1,1)上,f(x)单调增加当且仅当f′(x)=4(x-1)(3ax2+3ax-1)≥0,
即3ax2+3ax-1≤0,①
(ⅰ)当a=0时①恒成立;
(ⅱ)当a>0时①成立,当且仅当3a·12+3a·1-1≤0,解得 ;
;
(ⅲ)当a<0时①成立,即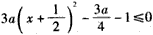 成立,
成立,
当且仅当 ,解得
,解得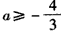 ;
;
综上,a的取值范围是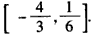 。
。
当a=
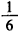 时,f′(x)=2(x+2)(x-1)2,
时,f′(x)=2(x+2)(x-1)2,当x<-2时,f′(x)<0,当x>-2时,f′(x)>0,
∴f(x)在(-∞,-2)内单调减,在(-2,+∞)内单调增,
∴在x=-2时,f(x)有极小值,
所以,f(-2)=-12是f(x)的极小值.
(Ⅱ)在(-1,1)上,f(x)单调增加当且仅当f′(x)=4(x-1)(3ax2+3ax-1)≥0,
即3ax2+3ax-1≤0,①
(ⅰ)当a=0时①恒成立;
(ⅱ)当a>0时①成立,当且仅当3a·12+3a·1-1≤0,解得
 ;
;(ⅲ)当a<0时①成立,即
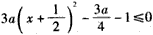 成立,
成立,当且仅当
 ,解得
,解得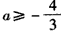 ;
;综上,a的取值范围是
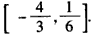 。
。 
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目