题目内容
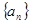 是正数等差数列,
是正数等差数列,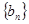 是正数等比数列,且a1=b1,a2n+1=b2n+1,则
是正数等比数列,且a1=b1,a2n+1=b2n+1,则
| A.an+1=bn+1 | B.an+1>bn+1 | C.an+1<bn+1 | D.an+1≥bn+1 |
D
解析

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
题目内容
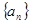 是正数等差数列,
是正数等差数列,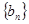 是正数等比数列,且a1=b1,a2n+1=b2n+1,则
是正数等比数列,且a1=b1,a2n+1=b2n+1,则
| A.an+1=bn+1 | B.an+1>bn+1 | C.an+1<bn+1 | D.an+1≥bn+1 |
D
解析

 备战中考寒假系列答案
备战中考寒假系列答案