题目内容
关于函数f(x)=4sin(2x+ ), (x∈R)有下列命题:
), (x∈R)有下列命题:
①y=f(x)是以2π为最小正周期的周期函数;
② y=f(x)可改写为y=4cos(2x- );
);
③y=f(x)的图象关于(- ,0)对称;
,0)对称;
④ y=f(x)的图象关于直线x=- 对称;
对称;
其中正确的序号为 .
②③.
解析试题分析:对于①,由三角函数的周期公式 ,故①不正确;对于②,因为
,故①不正确;对于②,因为 ,故②正确;对于③,当
,故②正确;对于③,当 时,
时, ,所以y=f(x)的图象关于(-
,所以y=f(x)的图象关于(- ,0)对称;对于④,当
,0)对称;对于④,当 时,
时, ,故④不正确.
,故④不正确.
考点:三角函数的周期公式 ,诱导公式,三角函数
,诱导公式,三角函数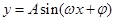 的对称轴与对称中心(本题还可以用公式完成检验,要注意三角函数
的对称轴与对称中心(本题还可以用公式完成检验,要注意三角函数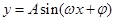 与x轴的交点一定是对称中心,而且对称轴对应的函数值一定是最大最小值).
与x轴的交点一定是对称中心,而且对称轴对应的函数值一定是最大最小值).

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知 =
= tan
tan -
- sin
sin +4(其中
+4(其中 、
、 为常数且
为常数且
 0),如果
0),如果 ,则
,则 (2010
(2010 -3)的值为 ( )
-3)的值为 ( )
| A.-3 | B.-5 | C.3 | D.5 |
 ,则
,则 __.
__. ,则
,则 .
.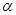 ,使
,使

 是偶函数
是偶函数 是第一象限的角,且
是第一象限的角,且 ,则
,则 .其中正确命题的序号是________________.
.其中正确命题的序号是________________. 的值为_________.
的值为_________. 的值域为 .
的值域为 . 的图象中相邻两个对称中心的距离为
的图象中相邻两个对称中心的距离为 ,②
,② 的图象关于点
的图象关于点 对称,③关于
对称,③关于 的方程
的方程 有且仅有一个实根,则
有且仅有一个实根,则 ,④命题
,④命题 对任意
对任意 ,都有
,都有 ;则
;则 存在
存在 .其中真命题的序号是_________________________ .
.其中真命题的序号是_________________________ . 在区间
在区间 上的所有解的和等于 .
上的所有解的和等于 .