题目内容
已知奇函数f(x)在区间(0,+∞)是增函数,则函数g(x)=f(|x|-1)的图象可能为( )
分析:根据函数的单调性排除不满足题意的选项,由函数的表达式g(x)=f(|x|-1)知其与函数y=f(x)的图象的关系,确定函数的图象特点,利用排除法推出正确结果.
解答:解:当x>0时,g(x)=f(|x|-1)=f(x-1),
∵f(x)在区间(0,+∞)是增函数
g(x)在(1,+∞)上是增函数,
故排除B,D.
根据奇函数f(x)在区间(0,+∞)是增函数得:
f(x)在区间(-∞,0)是减函数,
∴当1>x>0时,g(x)=f(|x|-1)=f(x-1)在(0,1)上是减函数,排除A,
则函数g(x)=f(|x|-1)的图象可能为C,
故选C
∵f(x)在区间(0,+∞)是增函数
g(x)在(1,+∞)上是增函数,
故排除B,D.
根据奇函数f(x)在区间(0,+∞)是增函数得:
f(x)在区间(-∞,0)是减函数,
∴当1>x>0时,g(x)=f(|x|-1)=f(x-1)在(0,1)上是减函数,排除A,
则函数g(x)=f(|x|-1)的图象可能为C,
故选C
点评:本题是基础题,考查读图能力,发现问题解决问题的能力,排除方法的应用,结合函数的单调性是解题的关键,好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知奇函数f(x)在[-1,0]上单调递减,又α,β为锐角三角形的两内角,则有( )
| A、f(sinα-sinβ)≥f(cosα-cosβ) | B、f(sinα-cosβ)>f(cosα-sinβ) | C、f(sinα-cosβ)≥f(cosα-sinβ) | D、f(sinα-cosβ)<f(cosα-sinβ) |
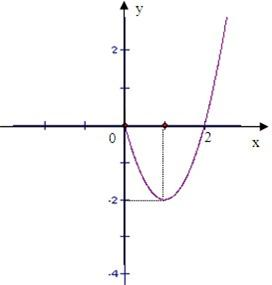 已知奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分,
已知奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分,