题目内容
已知 (x∈R)是偶函数.
(x∈R)是偶函数.
(Ⅰ)求实常数m的值,并给出函数f(x)的单调区间(不要求证明);
(Ⅱ)k为实常数,解关于x的不等式:f(x+k)>f(|3x+1|).
解:(Ⅰ)由题意得: ,
,
函数为偶函数,所以f(-1)=f(1),解得m=0
检验:当m=0时, ,f(-x)=f(x)成立,函数为偶函数
,f(-x)=f(x)成立,函数为偶函数
函数在区间(-∞,0)上是减函数,在区间(0,+∞)上是增函数
(Ⅱ)由(1)的单调性,可得f(x+k)>f(|3x+1|)等价于x+k>|3x+1|≥0或x+k<-|3x+1|<0,
转化为(x+k)2>(3x+1)2成立,因式分解为(4x+k+1)(2x-k+1)<0
讨论①当 时,不等式的解集为空集;
时,不等式的解集为空集;
②当 时,
时, ,不等式的解集为(
,不等式的解集为( );
);
③当 时,
时, ,不等式的解集为(
,不等式的解集为( )
)
综上所述,当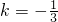 时,不等式的解集为空集;当
时,不等式的解集为空集;当 时,不等式的解集为(
时,不等式的解集为( );
);
当 时,不等式的解集为(
时,不等式的解集为( ).
).
分析:(Ⅰ)由偶函数的定义,取特殊值得关于m的方程f(-1)=f(1),解得m=0,最后检验所求出的值符合题意;
(Ⅱ)根据函数的单调性,将欲求解的不等式转化为|x+k|>|3x+1|,等价于不等式(x+k)2>(3x+1)2的求解,再根据相应方程根的情况讨论k值,从而得出不等式的解集.
点评:考查了函数的单调性与奇偶性,同时考查了含有参数的不等式的求解,属于中档题.
 ,
,
函数为偶函数,所以f(-1)=f(1),解得m=0
检验:当m=0时,
 ,f(-x)=f(x)成立,函数为偶函数
,f(-x)=f(x)成立,函数为偶函数函数在区间(-∞,0)上是减函数,在区间(0,+∞)上是增函数
(Ⅱ)由(1)的单调性,可得f(x+k)>f(|3x+1|)等价于x+k>|3x+1|≥0或x+k<-|3x+1|<0,
转化为(x+k)2>(3x+1)2成立,因式分解为(4x+k+1)(2x-k+1)<0
讨论①当
 时,不等式的解集为空集;
时,不等式的解集为空集;②当
 时,
时, ,不等式的解集为(
,不等式的解集为( );
);③当
 时,
时, ,不等式的解集为(
,不等式的解集为( )
)综上所述,当
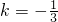 时,不等式的解集为空集;当
时,不等式的解集为空集;当 时,不等式的解集为(
时,不等式的解集为( );
);当
 时,不等式的解集为(
时,不等式的解集为( ).
).分析:(Ⅰ)由偶函数的定义,取特殊值得关于m的方程f(-1)=f(1),解得m=0,最后检验所求出的值符合题意;
(Ⅱ)根据函数的单调性,将欲求解的不等式转化为|x+k|>|3x+1|,等价于不等式(x+k)2>(3x+1)2的求解,再根据相应方程根的情况讨论k值,从而得出不等式的解集.
点评:考查了函数的单调性与奇偶性,同时考查了含有参数的不等式的求解,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目