题目内容
(13分)在中学阶段,对许多特定集合(如实数集、复数集以及平面向量集等)的学习常常是以定义运算(如四则运算)和研究运算律为主要内容.现设集合 由全体二元有序实数组组成,在
由全体二元有序实数组组成,在 上定义一个运算,记为
上定义一个运算,记为 ,对于
,对于 中的任意两个元素
中的任意两个元素 ,
, ,规定:
,规定:
 .
.
(1)计算:

 ;
;
(2)请用数学符号语言表述运算 满足交换律,并给出证明;
满足交换律,并给出证明;
(3)若“ 中的元素
中的元素 ”是“对
”是“对 ,都有
,都有




 成立”的充要条件,试求出元素
成立”的充要条件,试求出元素 .
.
 由全体二元有序实数组组成,在
由全体二元有序实数组组成,在 上定义一个运算,记为
上定义一个运算,记为 ,对于
,对于 中的任意两个元素
中的任意两个元素 ,
, ,规定:
,规定:
 .
.(1)计算:


 ;
;(2)请用数学符号语言表述运算
 满足交换律,并给出证明;
满足交换律,并给出证明;(3)若“
 中的元素
中的元素 ”是“对
”是“对 ,都有
,都有




 成立”的充要条件,试求出元素
成立”的充要条件,试求出元素 .
. (1)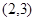

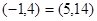 . (2)交换律:
. (2)交换律: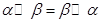 ,证明见解析;(3)
,证明见解析;(3)  .
.
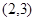

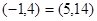 . (2)交换律:
. (2)交换律: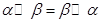 ,证明见解析;(3)
,证明见解析;(3)  .
.这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果.
(1)由已知α⊙β=(ad+bc,bd-ac),将:(2,3)⊙(-1,4)中参与运算的两个元素代入易得答案.
(2)根据已经学过的数、向量等的交换率,类比给出⊙运算的交换率,结合⊙的定义,不难证明.
(3)根据充要条件的定义,结合⊙的定义,不难得到一个关于I=(x,y)的方程组,解方程组,即可得到答案.
解:(1)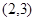

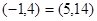 . ………3分
. ………3分
(2)交换律: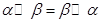 , ………4分
, ………4分
证明如下:设 ,
, ,则
,则
 ,
,

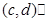
 =
=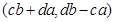 =
= .
.
∴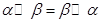 . ……… 8分
. ……… 8分
(3)设 中的元素
中的元素 ,对
,对 ,都有
,都有

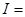
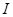

 成立,
成立,
由(2)知只需

 ,即
,即


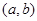
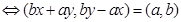
①若 ,显然有
,显然有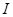

 成立;
成立;
②若 ,则
,则 ,解得
,解得 ,
,
∴当对 ,都有
,都有

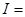
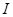

 成立时,得
成立时,得 ,
,
易验证当 时,有对
时,有对 ,都有
,都有

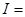
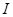

 成立………13分
成立………13分
∴ .
.
(1)由已知α⊙β=(ad+bc,bd-ac),将:(2,3)⊙(-1,4)中参与运算的两个元素代入易得答案.
(2)根据已经学过的数、向量等的交换率,类比给出⊙运算的交换率,结合⊙的定义,不难证明.
(3)根据充要条件的定义,结合⊙的定义,不难得到一个关于I=(x,y)的方程组,解方程组,即可得到答案.
解:(1)
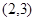

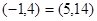 . ………3分
. ………3分(2)交换律:
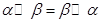 , ………4分
, ………4分证明如下:设
 ,
, ,则
,则
 ,
,
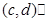
 =
=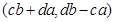 =
= .
.∴
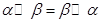 . ……… 8分
. ……… 8分 (3)设
 中的元素
中的元素 ,对
,对 ,都有
,都有

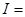
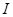

 成立,
成立,由(2)知只需


 ,即
,即


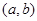
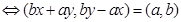
①若
 ,显然有
,显然有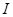

 成立;
成立; ②若
 ,则
,则 ,解得
,解得 ,
, ∴当对
 ,都有
,都有

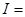
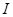

 成立时,得
成立时,得 ,
,易验证当
 时,有对
时,有对 ,都有
,都有

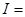
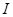

 成立………13分
成立………13分∴
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 {1,2,3,4,5}且若x∈M则6-x∈M,则满足条件的集合M有 个.
{1,2,3,4,5}且若x∈M则6-x∈M,则满足条件的集合M有 个. +
+ 的定义域为A,函数y=
的定义域为A,函数y= 的定义域为B.
的定义域为B. B,则x等于
B,则x等于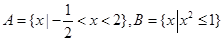 ,则
,则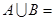 ( )
( )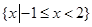

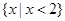

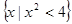 ,N=
,N=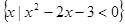 ,则集合M
,则集合M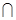 N=( )
N=( )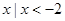 }
} }
} 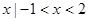 }
}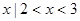 }
} ,则
,则 ( )
( ) ;
;  ;
;  ;
; ;
;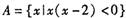 ,
,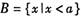 ,若A与B的
,若A与B的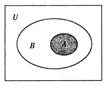




 的定义域为A,
的定义域为A,
 的定义域为B,且
的定义域为B,且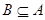 ,则实数
,则实数 的取值范围是( )
的取值范围是( )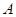 .
.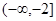
 .
. 
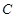 .
.
 .
.