题目内容
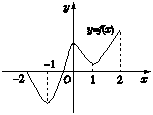
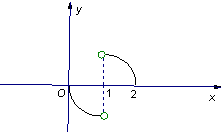 如图所示,函数y=f(x)的图象是圆心在点(1,
如图所示,函数y=f(x)的图象是圆心在点(1,(0,1)∪(
,2]
| 8 |
| 5 |
(0,1)∪(
,2]
.| 8 |
| 5 |
分析:首先由图象发现函数图象关于点(1,0)对称,从而有f(2-x)=-f(x),原不等式转化为:f(x)<
,然后在同一坐标系里作出y=
与原函数的图象,观察图象上位于直线下方的部分,找出对应的横坐标范围即可.
| x |
| 2 |
| x |
| 2 |
解答: 解:根据图象可得函数图象关于点(1,0)对称,从而有f(2-x)=-f(x),
解:根据图象可得函数图象关于点(1,0)对称,从而有f(2-x)=-f(x),
原不等式转化为:2f(x)<x,即f(x)<
,
由
⇒A(
,
)
得两图象在第一象限内的交点A为:
(
,
),
位于直线y=
下方的函数图象对应的横坐标范围是
(0,1)∪(
,2].
故答案为:(0,1)∪(
,2].
 解:根据图象可得函数图象关于点(1,0)对称,从而有f(2-x)=-f(x),
解:根据图象可得函数图象关于点(1,0)对称,从而有f(2-x)=-f(x),原不等式转化为:2f(x)<x,即f(x)<
| x |
| 2 |
由
|
| 8 |
| 5 |
| 4 |
| 5 |
得两图象在第一象限内的交点A为:
(
| 8 |
| 5 |
| 4 |
| 5 |
位于直线y=
| x |
| 2 |
(0,1)∪(
| 8 |
| 5 |
故答案为:(0,1)∪(
| 8 |
| 5 |
点评:本题考查了函数的对称性与函数的图象,用函数的性质解题等知识点,属于中档题.抓住函数的对称性质,是解决本题的关键所在.本题易因为不能由点的对称正确转化出方程导致无法下手

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 12、如图所示,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)=
12、如图所示,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)=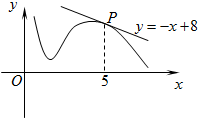
 f′(x)是函数y=f(x)的导函数,若y=f′(x)的图象如图所示则函数y=f(x)的图象可能是( )
f′(x)是函数y=f(x)的导函数,若y=f′(x)的图象如图所示则函数y=f(x)的图象可能是( )