题目内容
(本小题满分12分)
已知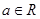 ,解不等式
,解不等式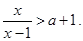
当 时原不等式的解集为
时原不等式的解集为 ;当
;当 时,解集为
时,解集为 ;
;
当 时,解集为
时,解集为 。
。
解析试题分析:原不等式可化为 ①
①
(1)当 时,原不等式为
时,原不等式为 ……2分
……2分
(2)当 时,原不等式化为
时,原不等式化为 . ② ……4分
. ② ……4分
当 时,原不等式等价于
时,原不等式等价于 ,由于
,由于 ,可解得
,可解得 ;
;
……8分
当 时,原不等式等价于
时,原不等式等价于 ,
,
由于 ,可解得
,可解得 或
或 ……10分
……10分
综上,当 时原不等式的解集为
时原不等式的解集为 ;
;
当 时,解集为
时,解集为 ;
;
当 时,解集为
时,解集为 . ……12分
. ……12分
考点:本小题主要考查含参数的不等式的解法.
点评:由于在①中,分子中 的系数中含有字母
的系数中含有字母 ,分类讨论就从这里引起。对于不等式②,分子中的系数
,分类讨论就从这里引起。对于不等式②,分子中的系数 不能随意约去,因为根据不等式的性质,若给不等式两边同时乘以一个负数,不等式的方向要改变.
不能随意约去,因为根据不等式的性质,若给不等式两边同时乘以一个负数,不等式的方向要改变.

练习册系列答案
相关题目
已知x>0,y>0,且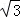 是3x与33y的等比中项,则
是3x与33y的等比中项,则 +
+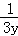 的最小值是( )
的最小值是( )
| A.2 | B.2 | C.4 | D.2 |
已知b>0,直线(b2+1)x+ay+2=0与直线x-b2y-1=0互相垂直,则ab的最小值等于( )
| A.1 | B.2 | C.2 | D.2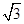 |
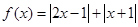
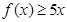 ;
;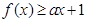 的解集为
的解集为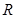 ,求实数
,求实数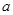 的取值范围
的取值范围 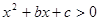 的解集为
的解集为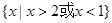
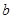 和
和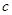 的值; (2)求不等式
的值; (2)求不等式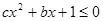 的解集.
的解集.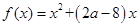 ,不等式
,不等式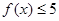 的解集是
的解集是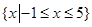 .
. 的值;
的值; 对于
对于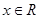 恒成立,求实数
恒成立,求实数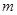 的取值范围.
的取值范围.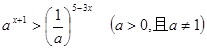 ,求
,求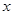 的取值范围.
的取值范围.  恒成立,记实数M的
恒成立,记实数M的