题目内容
(本小题满分12分)一个盒子中装有大小相同的2个红球和 个白球,从中任取2个球.
个白球,从中任取2个球.
(Ⅰ)若 ,求取到的2个球恰好是一个红球和一个白球的概率;
,求取到的2个球恰好是一个红球和一个白球的概率;
(Ⅱ)若取到的2个球中至少有1个红球的概率为 ,求
,求 .
.
【答案】
(1)若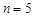 ,取到的2个球恰好是一个红球和一个白球的概率为
,取到的2个球恰好是一个红球和一个白球的概率为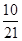 ;
;
(2)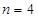 .
.
【解析】本试题主要是考查了古典概型概率的计算,以及组合数公式的灵活运用,问题,同时对立事件的概念和公式的灵活运用,是解决第二问的关键。
(1)因为一个盒子中装有大小相同的2个红球和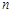 个白球,从中任取2个球.所有情况为
个白球,从中任取2个球.所有情况为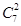
当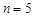 ,求取到的2个球恰好是一个红球和一个白球的情况有
,求取到的2个球恰好是一个红球和一个白球的情况有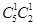 ;结合古典概型概率得到。
;结合古典概型概率得到。
(2)利用对立事件记“取到的2个球中至少有1个红球”为事件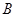 ,
,
由题意,得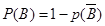 ,即为
,即为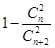 ,这样可以得到关于n的关系式,从而得到求解。
,这样可以得到关于n的关系式,从而得到求解。
解:(Ⅰ)记“取到的2个球恰好是一个红球和一个白球”为事件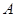 .
.
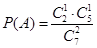
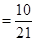
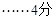
(Ⅱ)记“取到的2个球中至少有1个红球”为事件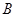 ,
,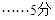
由题意,得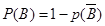

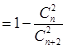
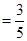
化简得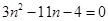 ,
,
解得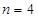 ,或
,或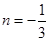 (舍去),
(舍去),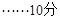
故 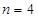 .
.
答:(1)若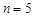 ,取到的2个球恰好是一个红球和一个白球的概率为
,取到的2个球恰好是一个红球和一个白球的概率为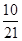 ;
;
(2)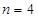 .
.

练习册系列答案
相关题目