题目内容
（不等式选讲）若实数a，b，c满足a2+b2+c2=4，则3a+4b+5c的最大值为______．
因为已知a、b、c是实数，且a2+b2+c2=4根据柯西不等式（a2+b2+c2）（x2+y2+z2）≥（ax+by+cz）2
故有（a2+b2+c2）（32+42+52）≥（3a+4b+5c）2
故（3a+4b+5c）2≤200，即3a+4b+5c≤10
即2a+b+2c的最大值为10
．
故答案为：10
．
故有（a2+b2+c2）（32+42+52）≥（3a+4b+5c）2
故（3a+4b+5c）2≤200，即3a+4b+5c≤10
| 2 |
即2a+b+2c的最大值为10
| 2 |
故答案为：10
| 2 |
练习册系列答案
相关题目
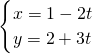（t为参数）与直线4x+ky=1垂直，则常数k=________．