Question

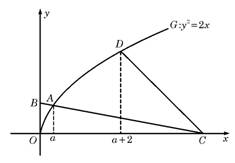
如图，曲线G的方程为y²=2x（ y≥0）．以原点为圆心，以t（t＞0）为半径的圆分别与曲线G和y轴的正半轴相交于点A与点B．直线AB与x轴相交于点C．
（Ⅰ）求点A的横坐标a与点C的横坐标c的关系式；
（Ⅱ）设曲线G上点D的横坐标为a+2，求证：直线CD的斜率为定值．

Answer 1

【答案】分析：（Ⅰ）先由点A在圆上得到a²+2a=t²．在利用A，B，C三点在一直线上，把t消去就可得到关于点A的横坐标a与点C的横坐标c的关系式；
（Ⅱ）由点D的横坐标为a+2代入曲线G的方程求出点D的坐标，再利用（Ⅰ）找到的点C（c，0），就可求出直线CD的斜率．
解答：解：（Ⅰ）由题意知，．
因为|OA|=t，所以a²+2a=t²．
由于t＞0，故有． （1）
由点B（0，t），C（c，0）的坐标知，
直线BC的方程为．
又因点A在直线BC上，故有，
将（1）代入上式，得，
解得．
（Ⅱ）因为，所以直线CD的斜率为．
所以直线CD的斜率为定值．
点评：本小题综合考查平面解析几何知识，主要涉及平面直角坐标系中的两点间距离公式、直线的方程与斜率、抛物线上的点与曲线方程的关系，考查运算能力与思维能力、综合分析问题的能力．