题目内容
①在直角坐标系中,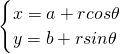 表示什么曲线?(其中a,b,r是常数,且r为正数,θ为变量.)
表示什么曲线?(其中a,b,r是常数,且r为正数,θ为变量.)
②若点P为圆C:(x-2)2+(y-3)2=4上任意一点,且O为原点,A(1,0),求 的取值范围.
的取值范围.
解:①∵a,b,r是常数,且r为正数,θ为变量,且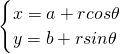 ,
,
∴有: ?(x-a)2+(y-b)2=r2. …(3分)
?(x-a)2+(y-b)2=r2. …(3分)
所以,在直角坐标系中,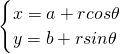 表示的是以(a,b)为圆心,r为半径的圆. …(6分)
表示的是以(a,b)为圆心,r为半径的圆. …(6分)
②∵点P为圆C:(x-2)2+(y-3)2=4上任意一点,故由①可设点P的坐标为(2+2cosθ,3+2sinθ). …(8分)
∴ ,
, . …(10分)
. …(10分)
故
 =
= …(12分)
…(12分)
又∵-1≤sin(θ+φ)≤1,∴ . …(13分)
. …(13分)
分析:①由cos2θ+cos2θ=1 消去θ,即得 曲线的直角坐标方程,从而得出表示什么曲线即可.
②根据点P为圆C:(x-2)2+(y-3)2=4上任意一点,故由①可设点P的坐标为(2+2cosθ,3+2sinθ),将向量用三角式表示,再利用向量的数量积公式结合三角函数的性质即可求出 的取值范围.
的取值范围.
点评:本题考查轨迹方程、圆的参数方程,把参数方程化为普通方程的方法,两个向量的数量积,正弦函数的值域,
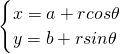 ,
,∴有:
 ?(x-a)2+(y-b)2=r2. …(3分)
?(x-a)2+(y-b)2=r2. …(3分)所以,在直角坐标系中,
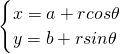 表示的是以(a,b)为圆心,r为半径的圆. …(6分)
表示的是以(a,b)为圆心,r为半径的圆. …(6分)②∵点P为圆C:(x-2)2+(y-3)2=4上任意一点,故由①可设点P的坐标为(2+2cosθ,3+2sinθ). …(8分)
∴
 ,
, . …(10分)
. …(10分)故

 =
= …(12分)
…(12分)又∵-1≤sin(θ+φ)≤1,∴
 . …(13分)
. …(13分)分析:①由cos2θ+cos2θ=1 消去θ,即得 曲线的直角坐标方程,从而得出表示什么曲线即可.
②根据点P为圆C:(x-2)2+(y-3)2=4上任意一点,故由①可设点P的坐标为(2+2cosθ,3+2sinθ),将向量用三角式表示,再利用向量的数量积公式结合三角函数的性质即可求出
 的取值范围.
的取值范围.点评:本题考查轨迹方程、圆的参数方程,把参数方程化为普通方程的方法,两个向量的数量积,正弦函数的值域,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某种股票的价格y(元)在一年内与月份x(月)之间的函数关系如下表:
某种股票的价格y(元)在一年内与月份x(月)之间的函数关系如下表:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 10.1 | 10.2 | 10.4 | 10.8 | 11.6 | 13.2 | 16.4 |
(Ⅱ)预测这种股票在8月份时的价格,以及价格为112.4元时的月份.
已知x,y之间的一组数据如下表:
(1)以x为横坐标,y为纵坐标在直角坐标系中画出散点图,并说明这两个变量之间的关系是正相关关系还是负相关关系.
(2)求线性回归方程.(参考公式: )
)
| x | 1 | 3 | 6 | 7 | 8 |
| y | 1 | 2 | 3 | 4 | 5 |
(2)求线性回归方程.(参考公式:
 )
)
某种股票的价格y(元)在一年内与月份x(月)之间的函数关系如下表:
(Ⅰ)在直角坐标系中,通过描点、连线,猜测并确定y与x之间的函数关系式;
(Ⅱ)预测这种股票在8月份时的价格,以及价格为112.4元时的月份.

| x | 1 | 2 | 3 | 4 | 5 | 6 | |
| y | 10.1 | 10.2 | 10.4 | 10.8 | 11.6 | 13.2 | 16.4 |
(Ⅱ)预测这种股票在8月份时的价格,以及价格为112.4元时的月份.



 某种股票的价格y(元)在一年内与月份x(月)之间的函数关系如下表:
某种股票的价格y(元)在一年内与月份x(月)之间的函数关系如下表: