Question

（2013•温州一模）正方体ABCD-A₁B₁C₁D₁中，二面角C₁-A₁B-D的余弦值为

1

3

．

Answer 1

分析：通过建立空间直角坐标系，利用两个平面的法向量的夹角即可得出二面角．

解答：解：如图所示，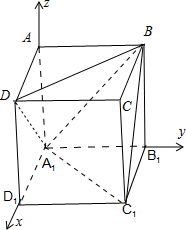
不妨设棱长AB=1，则A₁（0，0，0），B（0，1，1），D（1，0，1），C₁（1，1，0）．
则

A1B

=(0，1，1)，

BD

=(1，-1，0)，

A1C1

=(1，1，0)．
设平面A₁BD的法向量为

n

=(x，y，z)，则

n • A1B =y+z=0 n • BD =x-y=0

，令x=1，则y=1，z=-1．
∴

n

=(1，1，-1)．
设平面A₁BC₁的法向量为

m

=(a，b，c)，则

m • A1B =b+c=0 m • A1C1 =a+b=0

，令a=1，则b=-1，z=1．
∴

m

=(1，-1，1)．
∴cos＜

m

，

n

＞=

m • n

| m | | n |

=

1

3 × 3

=

1

3

．
从图上看二面角C₁-A₁B-D的平面角是一个锐角，故其余弦值为

1

3

．

点评：本题考查了通过建立空间直角坐标系，利用两个平面的法向量的夹角得出二面角的方法．必须熟练掌握．