题目内容
( 9分) 如图,过椭圆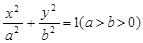 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆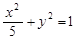 的“左特征点”M的坐标;
的“左特征点”M的坐标;

【答案】
(1)解:设M(m,0)为椭圆 的左特征点,
的左特征点,
椭圆的左焦点为 ,设直线AB的方程为
,设直线AB的方程为
将它代入 得:
得: ,
,
即
设A(x1,y1),B(x2,y2),则 ,
,
∵∠AMB被x轴平分,∴
即 ,Þ
,Þ 
Þ 
∴ , 于是
, 于是
∵ ,∴
,∴ ,即
,即 ∴M(
∴M( ,0)
,0)
【解析】略

练习册系列答案
相关题目
 ,液晶广告屏幕MNEF的面积为
,液晶广告屏幕MNEF的面积为

 ,液晶广告屏幕MNEF的面积为
,液晶广告屏幕MNEF的面积为
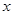 的函数关系式,并与出该函数的定义域;
的函数关系式,并与出该函数的定义域;
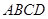 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求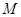 在
在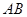 的延长线上,
的延长线上,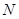 在
在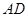 的延长线上,且对角线
的延长线上,且对角线 过
过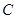 点.已知
点.已知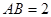 米,
米,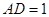 米.
米.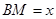 (单位:米),要使花坛
(单位:米),要使花坛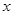 的取值范围;
的取值范围;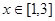 (单位:米),则当
(单位:米),则当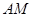 ,
,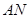 的长度分别是多少时,花坛
的长度分别是多少时,花坛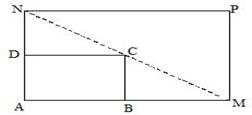
 如图,已知椭圆
如图,已知椭圆