题目内容
13.如图,已知长方形ABCD中,AB=2,A1,B1分别是AD,BC边上的点,且AA1=BB1=1,E,F分别为B1D与AB的中点.把长方形ABCD沿直线A1B1折成直角二面角,且∠A1B1D=30°.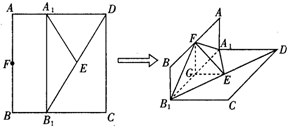
(1)求证:CD⊥EF
(2)求三棱锥A1-B1EF的体积.
分析 (I)证明AA1⊥A1B1,取A1B1的中点G,边接EG,FG,推出FG⊥A1B1,EG⊥A1B1,即可证明A1B1⊥面EFG,然后证明CD⊥EF.
(II)通过二面角A-A1B1-D为直二面角,利用FG⊥面A1B1E,然后求解几何体的体积.
解答 解:(I)证明:因为AA1=BB1=1,且AA1∥BB1,所以四边形ABB1A1为矩形,故AA1⊥A1B1,
取A1B1的中点G,边接EG,FG,因为F为AB的中点,所以AF∥A1G,且AF=A1G,
可得四边形AFGA1是平行四边形,所以FG∥AA1,故FG⊥A1B1,
同理可得EG⊥A1B1,所以A1B1⊥面EFG,可得A1B1⊥EF.
因为CD∥A1B1,所以CD⊥EF.(6分)
(II)因为∠A1B1D=30°,所以$tan{30°}=\frac{{{A_1}D}}{{{A_1}{B_1}}}=\frac{{{A_1}D}}{2}$,
可得${A_1}D=\frac{{2\sqrt{3}}}{3},EG=\frac{1}{2}{A_1}D=\frac{{\sqrt{3}}}{3}$,
因为二面角A-A1B1-D为直二面角,由(I)可知FG⊥面A1B1E,
所以${V_{{A_1}-{B_1}EF}}={V_{F-{A_1}{B_1}E}}=\frac{1}{3}×1×\frac{1}{2}×\frac{{\sqrt{3}}}{3}×2=\frac{{\sqrt{3}}}{9}$(12分)
点评 本题考查直线与平面垂直的判定定理以及性质定理的应用,几何体的体积的求法,考查计算能力以及空间想象能力.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
3.已知函数f(x)=|x|-1,若关于x的方程f2(x)+(2m-1)f(x)+4-2m=0有四个不同的实数解,则实数m的取值范围是( )
| A. | m<-2 | B. | m<-2.5 | C. | m<1.5 | D. | m>1.5 |
18.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的外接球的表面积为( )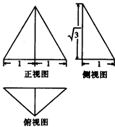

| A. | $\frac{{\sqrt{3}}}{3}π$ | B. | $\frac{16}{3}π$ | C. | $\frac{26}{3}π$ | D. | $\frac{{32\sqrt{3}}}{27}π$ |