题目内容
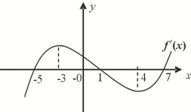
函数f(x)的导函数y=f/(x)的图象如下图,则函数f(x)的单调递增区间为 ________.

[-1,0]和[2,+∞)
分析:导函数在某个区间上的函数值的符号是这样对应的,导数值为负,则函数在这个区间上是减函数,若导数为正,则函数在这个区间上是增函数,由此规则可以看到导数为正的区间有两个,由图定出即可.
解答:由图象可以看出在[-1,0]和[2,+∞)上,f/(x)≥0.
故数f(x)的单调递增区间为[-1,0]和[2,+∞)
故答案为[-1,0]和[2,+∞).
点评:本题考点是函数的单调性与单调区间,考查由导函数的图象判断函数的单调区间,这是导数的一个非常重要的运用,解答本题时有一个需要注意,那就是单调区间写成开区间还是闭区间的问题,一般要求是这样的如果在端点处函数有意义,一般将其写为闭区间,否则为开区间,如[2,+∞)的右端点,就只能写成开的形式.
分析:导函数在某个区间上的函数值的符号是这样对应的,导数值为负,则函数在这个区间上是减函数,若导数为正,则函数在这个区间上是增函数,由此规则可以看到导数为正的区间有两个,由图定出即可.
解答:由图象可以看出在[-1,0]和[2,+∞)上,f/(x)≥0.
故数f(x)的单调递增区间为[-1,0]和[2,+∞)
故答案为[-1,0]和[2,+∞).
点评:本题考点是函数的单调性与单调区间,考查由导函数的图象判断函数的单调区间,这是导数的一个非常重要的运用,解答本题时有一个需要注意,那就是单调区间写成开区间还是闭区间的问题,一般要求是这样的如果在端点处函数有意义,一般将其写为闭区间,否则为开区间,如[2,+∞)的右端点,就只能写成开的形式.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,
已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,| x | -2 | 0 | 4 |
| f(x) | 1 | -1 | 1 |
| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|
 4、已知函数f(x)的导函数的图象如图所示,给出下列四个结论:
4、已知函数f(x)的导函数的图象如图所示,给出下列四个结论: