题目内容
已知函数f(x)=lg(ax2+2x+1).(1)若函数f(x)的定义域为R，求实数a的取值范围，并求此时函数的值域;
(2)若函数f(x)的值域为R，求实数a的取值范围，并求此时函数的定义域.
解：函数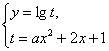
复合而成.
当a≠0时，ax2+2x+1=a(x+
)2+1-
.
(1)若函数f(x)的定义域为R，则对x∈R,t=ax2+2x+1＞0恒成立，从而a=0时,t=2x+1＞0，定义域不为R，∴a≠0.
则有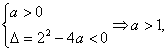
此时t=a(x+
)+1-
≥1-
,则y≥lg(1-
).
∴f(x)定义域为R时，a的取值范围是(1,+∞)，此时函数值域为［lg(1-
),+∞).
(2)若f(x)值域为R，则t=ax2+2x+1要取遍全体正数.
当a=0时，t=2x+1可取遍全体正数，满足条件，此时x＞-
.
当a≠0时，t=ax2+2x+1若取遍全体正数，需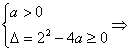
0＜a≤1.
此时，若ax2+2x+1＞0,则x＜
.
∴f(x)的值域为R时，a的取值范围是［0,1］.
其中a=0时，f(x)的定义域为(
,+∞),0＜a≤1时，f(x)的定义域为(-∞,
)∪(
,+∞).
练习册系列答案
相关题目