题目内容
在面积为S的正三角形ABC中,E是边AB上的动点,过点E作EF∥BC,交AC于点F,当点E运动到离边BC的距离为△ABC高的
时,△EFB的面积取得最大值为
S.类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于______V.
| 1 |
| 2 |
| 1 |
| 4 |

根据几何体和平面图形的类比关系,
三角形的边应与四面体中的各个面进行类比,而面积与体积进行类比,中位线与中截面进行类比:
在面积为S的正三角形ABC中,当点E运动到离边BC的距离为△ABC高的
| 1 |
| 2 |
| 1 |
| 4 |
类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,设AE=xAB(0<x<1),则四面体EFGB的体积V1=x2(1-x)V=
| 1 |
| 2 |
| 1 |
| 2 |
| x+x+2-2x |
| 3 |
| 4 |
| 27 |
| 4 |
| 27 |
故答案为:
| 4 |
| 27 |

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 时,△EFB的面积取得最大值为
时,△EFB的面积取得最大值为 .类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V.
.类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V. 时,△EFB的面积取得最大值为
时,△EFB的面积取得最大值为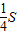 .类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V.
.类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V. 时,△EFB的面积取得最大值为
时,△EFB的面积取得最大值为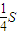 .类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V.
.类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V.