题目内容

已知△ABC中，内角A、B、C的对边的边长为a、b、c，且bcosC=（2a-c）cosB，则y=cos²A+cos²C的最小值为________．

$\text{[math]}$
分析：△ABC中，由正弦定理可求得cosB= $\text{[math]}$ ，从而求得 B= $\text{[math]}$ ，A+C= $\text{[math]}$ ．利用两角和差的正弦公式，二倍角公式化简 y=cos²A+cos²C=1- $\text{[math]}$ sin（2A- $\text{[math]}$ ），再由
- $\text{[math]}$ ＜2A- $\text{[math]}$ ＜ $\text{[math]}$ ，求得- $\text{[math]}$ ＜sin（2A- $\text{[math]}$ ）≤1，由此可得y的最小值．
解答：△ABC中，由正弦定理可得：sinBcosC=2sinAcosB-sinCcosB，即sin（B+C）=2sinAcosB．
因为0＜A＜π，所以sinA≠0，∴cosB= $\text{[math]}$ ，∴B= $\text{[math]}$ ，A+C= $\text{[math]}$ ．
∴2A+2C= $\text{[math]}$ ，则y=cos²A+cos²C= $\text{[math]}$ + $\text{[math]}$ = $\text{[math]}$ + $\text{[math]}$ =1+ $\text{[math]}$ [ $\text{[math]}$ cos2A- $\text{[math]}$ sin2A]
=1- $\text{[math]}$ sin（2A- $\text{[math]}$ ）．
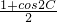∵0＜2A＜ $\text{[math]}$ ，∴- $\text{[math]}$ ＜2A- $\text{[math]}$ ＜ $\text{[math]}$ ，则- $\text{[math]}$ ＜sin（2A- $\text{[math]}$ ）≤1，
故y=cos²A+cos²C的最小值为 1- $\text{[math]}$ = $\text{[math]}$ ，
故答案为 $\text{[math]}$ ．
点评：本题主要考查正弦定理的应用，两角和差的正弦公式，二倍角公式以及诱导公式的应用，属于中档题．