题目内容
函数f（x）=|log3x|在区间[a，b]上的值域为[0，1]，则b-a的最小值为
．
| 2 |
| 3 |
| 2 |
| 3 |
分析：先画出函数图象，再数形结合得到a、b的范围，最后计算b-a的最小值即可
解答：解：函数f（x）=|log3x|的图象如图
而f（
）=f（3）=1
由图可知a∈[
，1]，b∈[1，3]
b-a的最小值为a=
，b=1时，即b-a=
故答案为
而f（
| 1 |
| 3 |
由图可知a∈[
| 1 |
| 3 |
b-a的最小值为a=
| 1 |
| 3 |
| 2 |
| 3 |
故答案为
| 2 |
| 3 |
点评：本题考查了数形结合解决函数问题的方法，解题时要准确画图，精确分析，善于用形解决代数问题
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
的定义域为M，g(x)＝lo
(2＋x＝6x2)的单调递减区间是开区间N，设全集U＝R，则M∩CU(N)＝________．
）2+7lo
+3≤0的解集为M，求当x∈M时，函数f（x）=（lo
）（lo
）的最大值和最小值．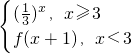
，则f（2+lo
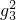）的值为________．