题目内容
已知函数f(x)=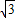 sin(2x-
sin(2x-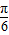 )+2sin2(x-
)+2sin2(x-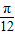 ) (x∈R).
) (x∈R).(1)求函数f(x)的最小正周期;
(2)求使函数f(x)取得最大值的x的集合.
【答案】分析:(1)先将函数f(x)化简为:f(x)=2sin(2x-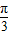 )+1,根据T=
)+1,根据T=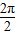 =π得到答案.
=π得到答案.
(2)因为f(x)取最大值时应该有sin(2x-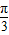 )=1成立,即2x-
)=1成立,即2x-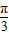 =2kπ+
=2kπ+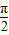 ,可得答案.
,可得答案.
解答:解:(1)f(x)=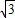 sin(2x-
sin(2x-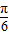 )+1-cos2(x-
)+1-cos2(x-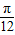 )
)
=2[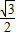 sin2(x-
sin2(x-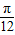 )-
)- cos2(x-
cos2(x-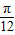 )]+1
)]+1
=2sin[2(x-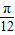 )-
)-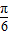 ]+1
]+1
=2sin(2x-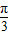 )+1
)+1
∴T=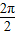 =π
=π
(2)当f(x)取最大值时,sin(2x-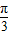 )=1,有2x-
)=1,有2x-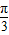 =2kπ+
=2kπ+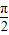
即x=kπ+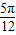 (k∈Z)
(k∈Z)
∴所求x的集合为{x∈R|x=kπ+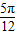 ,(k∈Z)}.
,(k∈Z)}.
点评:本题主要考查三角函数的最小正周期的求法和三角函数的最值问题.属基础题.
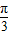 )+1,根据T=
)+1,根据T=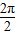 =π得到答案.
=π得到答案.(2)因为f(x)取最大值时应该有sin(2x-
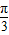 )=1成立,即2x-
)=1成立,即2x-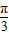 =2kπ+
=2kπ+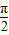 ,可得答案.
,可得答案.解答:解:(1)f(x)=
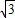 sin(2x-
sin(2x-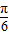 )+1-cos2(x-
)+1-cos2(x-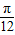 )
)=2[
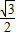 sin2(x-
sin2(x-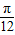 )-
)- cos2(x-
cos2(x-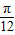 )]+1
)]+1=2sin[2(x-
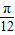 )-
)-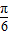 ]+1
]+1=2sin(2x-
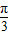 )+1
)+1∴T=
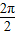 =π
=π(2)当f(x)取最大值时,sin(2x-
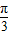 )=1,有2x-
)=1,有2x-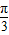 =2kπ+
=2kπ+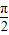
即x=kπ+
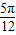 (k∈Z)
(k∈Z)∴所求x的集合为{x∈R|x=kπ+
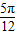 ,(k∈Z)}.
,(k∈Z)}.点评:本题主要考查三角函数的最小正周期的求法和三角函数的最值问题.属基础题.

练习册系列答案
相关题目
