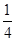题目内容
在直角三角形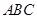 中,
中,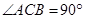 ,
,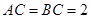 ,点
,点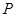 是斜边
是斜边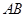 上的一个三等分点,则
上的一个三等分点,则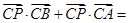 ( )
( )
| A.0 | B.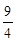 | C.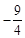 | D.4 |
D
解析试题分析:由于点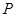 是斜边
是斜边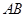 上的一个三等分点,不妨设
上的一个三等分点,不妨设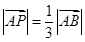 ,将
,将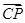 改写为
改写为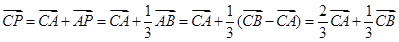 ,再利用
,再利用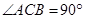 ,于是
,于是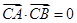 ,又根据
,又根据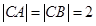 ,因此
,因此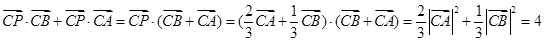 .
.
考点:向量的三角形法则、数量积.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
设向量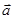 与
与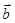 满足
满足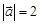 ,
,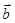 在
在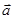 方向上的投影为
方向上的投影为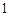 ,若存在实数
,若存在实数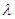 ,使得
,使得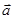 与
与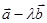 垂直,则
垂直,则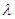 =( )
=( )
A.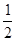 | B.1 | C. 2 | D.3 |
已知向量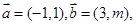 若
若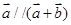 ,则m=( )
,则m=( )
A.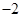 | B.2 | C.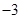 | D.3 |
已知向量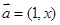 ,
,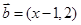 ,若
,若 ,则
,则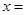 ( )
( )
| A.-1或2 | B.-2或1 | C.1或2 | D.-1或-2 |
在平行四边形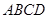 中,
中,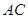 为一条对角线,
为一条对角线, ,则
,则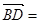 ( )
( )
A.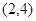 | B.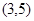 | C.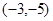 | D.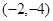 |
已知非零向量a,b满足向量a+b与向量a-b的夹角为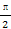 ,那么下列结论中一定成立的是( )
,那么下列结论中一定成立的是( )
| A.a=b | B.|a|=|b| |
| C.a⊥b | D.a∥b |
已知向量a=(1,2),b=(1,0),c=(3,4).若λ为实数,(a+λb)∥c,则λ等于( )
A.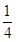 | B.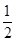 | C.1 | D.2 |
已知O,A,M,B为平面上不同的四点,且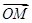 =λ
=λ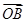 +(1-λ)
+(1-λ)  ,λ∈(1,2),则( ).
,λ∈(1,2),则( ).
| A.点M在线段AB上 |
| B.点B在线段AM上 |
| C.点A在线段BM上 |
| D.O,A,M,B四点共线 |
 中,
中, 边的中点,过点
边的中点,过点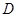 的直线分别交直线
的直线分别交直线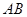 、
、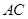 于点
于点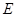 、
、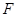 ,若
,若 ,
,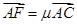 ,其中
,其中 ,则
,则 的最小值是( )
的最小值是( )