题目内容
定义在R上的二次函数y=f(x)在(0,2)上单调递减,其图象关于直线x=2对称,则下列式子可以成立的是( )
A、f(
| ||||
B、f(3)<f(
| ||||
C、f(3)<f(
| ||||
D、f(
|
分析:由于图象关于直线x=2对称,所以有f(
)=f(
),f(3)=f(1),又因为0<
<1<
<2,且函数在(0,3)内单调递减,从而判断大小.
| 5 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:由于y=f(x)关于直线x=2对称,故f(
)=f(
),f(3)=f(1),
由于f(x)在(0,2)上单调递减,故f(
)<f(1)<f(
),即f(
) <f( 3) <f(
)
故选D.
| 5 |
| 2 |
| 3 |
| 2 |
由于f(x)在(0,2)上单调递减,故f(
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
故选D.
点评:本题主要考查了函数的对称性单调性的综合运用,利用对称性把所要比较的变量转化到同一单调区间,利用函数的单调性比较函数值的大小,是解决此类问题的常用方法.

练习册系列答案
相关题目
 (2011•南通模拟)
(2011•南通模拟)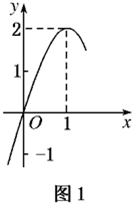 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.