Question

(1)已知α+β=45°,求(1+tanα)(1+tanβ)的值.

(2)已知sin(α+β)=,sin(α-β)=,求.

Answer 1

解:(1)∵α+β=45°,

∴tan(α+β)=tan45°=1.

又∵tan(α+β)=,

∴tanα+tanβ=tan(α+β)(1-tanαtanβ),

即tanα+tanβ=1-tanαtanβ.

∴原式=1+tanα+tanβ+tanαtanβ=1+(1-tanαtanβ)+tanαtanβ=2.

(2)∵sin(α+β)=,sin(α-β)=,

∴sinαcosβ+cosαsinβ=.①

sinαcosβ-cosαsinβ=.②

①+②,得sinαcosβ=,

①-②,得cosαsinβ=,

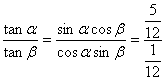∴=5.

点评:本题都是公式的变形应用,像(1)中当出现α+β为特殊角时,就可以考虑逆用两角和的正切公式的变形式tanα+tanβ=tan(α+β)(1-tanαtanβ),这个变形式子对我们解题很有用处.而(2)中化切为弦的求法更是巧妙,解完后留出一定的时间让学生认真总结反思,熟练掌握其变化的思想方法.