题目内容
{a,b}?{0,1,2,3,5},由ax+by=0确定直线和(x+2)2+(y-1)2=1相交的概率为
.
| 2 |
| 5 |
| 2 |
| 5 |
分析:如图所示,由题意得直线的斜率为-
,直线是必过原点的,先求出OB的斜率为-
,OA的斜率为0,直线和圆相交等价于0>-
>-
,即
>
>0,所有(a,b) 的取法共25种,其中满足0>-
>-
,即
>
>0的取法,有10种,
由此求得所求事件的概率.
| a |
| b |
| 4 |
| 3 |
| a |
| b |
| 4 |
| 3 |
| 4 |
| 3 |
| a |
| b |
| a |
| b |
| 4 |
| 3 |
| 4 |
| 3 |
| a |
| b |
由此求得所求事件的概率.
解答: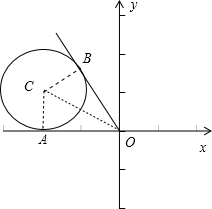 解:如图所示:由题意得直线的斜率为-
解:如图所示:由题意得直线的斜率为-
,直线是必过原点的,
根据圆心C(-2,1)到直线OB:y=kx 的距离等于半径1可得
1=
,解得k=-
或0.
故当 0>-
>-
时,圆心到直线的距离小于半径,
此时,直线ax+by=0 和圆(x+2)2+(y-1)2=1相交.
即当 0<
<
时,ax+by=0 和(x+2)2+(y-1)2=1相交.
由于(a,b)的所有取法共有5×5=25种,
其中,满足0>-
>-
,即
>
>0的取法(a,b) 有:
(1,1)、(1,2)、(1,3)、(1,5)、
(2,2)、(2,3)、(2,5)、(3,3)、(3,5),(5,5),共10种,
故所求事件的概率为:
=
,
故答案为:
.
 解:如图所示:由题意得直线的斜率为-
解:如图所示:由题意得直线的斜率为-| a |
| b |
根据圆心C(-2,1)到直线OB:y=kx 的距离等于半径1可得
1=
| |-2k-1| | ||
|
| 4 |
| 3 |
故当 0>-
| a |
| b |
| 4 |
| 3 |
此时,直线ax+by=0 和圆(x+2)2+(y-1)2=1相交.
即当 0<
| a |
| b |
| 4 |
| 3 |
由于(a,b)的所有取法共有5×5=25种,
其中,满足0>-
| a |
| b |
| 4 |
| 3 |
| 4 |
| 3 |
| a |
| b |
(1,1)、(1,2)、(1,3)、(1,5)、
(2,2)、(2,3)、(2,5)、(3,3)、(3,5),(5,5),共10种,
故所求事件的概率为:
| 10 |
| 25 |
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:本题主要考查直线和圆相交的性质,点到直线的距离公式的应用,体现了数形结合和等价转化的数学思想,
注意不能包括直线和圆相切的情况,属于中档题.
注意不能包括直线和圆相切的情况,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
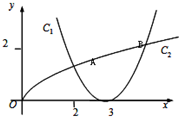 函数f(x)=(x-3)2和g(x)=
函数f(x)=(x-3)2和g(x)=