题目内容
已知A、B、C是三角形ABC的三内角,且 =(sinB-sinA,sinB-sinC),
=(sinB-sinA,sinB-sinC), =(sinB+sinA,-sinC),并且
=(sinB+sinA,-sinC),并且 •
• =0.
=0.
(1)求角A的大小.
(2)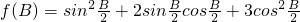 ,求f(B)的递增区间.
,求f(B)的递增区间.
解:(1)由 •
• =0
=0
得(sinB-sinA)(sinB+sinA)-sinC(sinB-sinC)=0
即sin2B-sin2A-sinBsinC+sin2C=0(2分)
由正弦定理得b2-a2+bc+c2=0
即b2+c2-a2=bc(4分)
由余弦定理得
又0<A<π,所以 (6分)
(6分)
(2) =cosB+sinB+2=
=cosB+sinB+2= ,(8分)
,(8分)
因为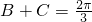 ,且B,C均为△ABC的内角,
,且B,C均为△ABC的内角,
所以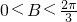 ,
,
所以 ,
,
又 ,
,
即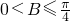 时,f(B)为递增函数,
时,f(B)为递增函数,
即f(B)的递增区间为 (12分)
(12分)
分析:(1)利用 •
• =0,推出sin2B-sin2A-sinBsinC+sin2C=0,由正弦定理得b2-a2+bc+c2=0,然后利用余弦定理求出角A的大小.
=0,推出sin2B-sin2A-sinBsinC+sin2C=0,由正弦定理得b2-a2+bc+c2=0,然后利用余弦定理求出角A的大小.
(2)化简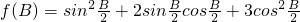 为
为 ,根据B+C的范围得到
,根据B+C的范围得到 ,求出函数f(B)的递增区间.
,求出函数f(B)的递增区间.
点评:本题考查正弦函数的单调性,同角三角函数间的基本关系,考查计算能力,是中档题.
 •
• =0
=0得(sinB-sinA)(sinB+sinA)-sinC(sinB-sinC)=0
即sin2B-sin2A-sinBsinC+sin2C=0(2分)
由正弦定理得b2-a2+bc+c2=0
即b2+c2-a2=bc(4分)
由余弦定理得

又0<A<π,所以
 (6分)
(6分)(2)
 =cosB+sinB+2=
=cosB+sinB+2= ,(8分)
,(8分)因为
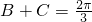 ,且B,C均为△ABC的内角,
,且B,C均为△ABC的内角,所以
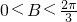 ,
,所以
 ,
,又
 ,
,即
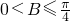 时,f(B)为递增函数,
时,f(B)为递增函数,即f(B)的递增区间为
 (12分)
(12分)分析:(1)利用
 •
• =0,推出sin2B-sin2A-sinBsinC+sin2C=0,由正弦定理得b2-a2+bc+c2=0,然后利用余弦定理求出角A的大小.
=0,推出sin2B-sin2A-sinBsinC+sin2C=0,由正弦定理得b2-a2+bc+c2=0,然后利用余弦定理求出角A的大小.(2)化简
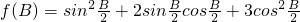 为
为 ,根据B+C的范围得到
,根据B+C的范围得到 ,求出函数f(B)的递增区间.
,求出函数f(B)的递增区间.点评:本题考查正弦函数的单调性,同角三角函数间的基本关系,考查计算能力,是中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 中的最大数为
中的最大数为 ,最小数为
,最小数为 已知
已知 的三边边长为a,b,c(
的三边边长为a,b,c( ),定义它的倾斜度为
),定义它的倾斜度为
 是“
是“ ,则△ABC为( )
,则△ABC为( ) ,则△ABC为( )
,则△ABC为( )