题目内容
1.已知递增数列{an}各项均是正整数,且满足a${\;}_{{a}_{n}}$=3n,则a5的值为( )| A. | 2 | B. | 6 | C. | 8 | D. | 9 |
分析 运用a${\;}_{{a}_{n}}$=3n,递推得出a1=1,a1≥3不符合题意,
讨论得出a1=2,再运用递推关系式对称a2=3,a2=3,a6=9,根据不等式得出a3<a4<a5<a6
求解即可得出a5=8.
解答 解:∵a${\;}_{{a}_{n}}$=3n,
∴a${\;}_{{a}_{1}}$=3×1=3,
若a1=1,则a${\;}_{{a}_{1}}$=a1=1,与a${\;}_{{a}_{1}}$=3×1=3矛盾,
若a1≥3,则a${\;}_{{a}_{1}}$≥a3,而a${\;}_{{a}_{1}}$=3,所以3≥a3,即a1≥a3与数列{an}递增矛盾,
于是a1=2,得a${\;}_{{a}_{1}}$=a2=3×1=3,a2=3,
a${\;}_{{a}_{2}}$=a3=3×2=6,
a${\;}_{{a}_{3}}$=a6=3×3=9,而a3<a4<a5<a6
∵递增数列{an}各项均是正整数
∴a4=7,a5=8,所以a5=8.
故选:C.
点评 本题综合考查了数列的函数性质,递推关系式的运用,分类讨论的思想,属于中档题,关键是判断得出a1=2,递推即可.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
11.一个算法的程序框图如图所示,若该程序输出的结果为$\frac{5}{6}$,则判断框中应填入的条件是( )


| A. | i<4 | B. | i<5 | C. | i≥5 | D. | i<6 |
12.抛物线y=$\frac{1}{8}$x2上到焦点的距离等于10的点的坐标为( )
| A. | (-8,8) | B. | (8,8) | C. | (-8,-8)或(8,-8) | D. | (-8,8)或(8,8) |
16.集合A={0,2},B={1,a2},若A∪B={0,1,2,4},则实数a的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\sqrt{2}$ |
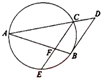 如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.