题目内容
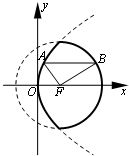（2012•黄浦区二模）已知△FAB，点F的坐标为（1，0），点A、B分别在图中抛物线y2=4x及圆（x-1）2+y2=4的实线部分上运动，且AB总是平行于x轴，那么△FAB的周长的取值范围为（4，6）
（4，6）
．分析：由抛物线定义可得|AF|=xA+1，从而△FAB的周长=|AF|+|AB|+|BF|=xA+1+（xB-xA）+2=3+xB，确定B点横坐标的范围，即可得到结论．
解答：解：抛物线的准线l：x=-1，焦点F（1，0），由抛物线定义可得|AF|=xA+1，
∴△FAB的周长=|AF|+|AB|+|BF|=xA+1+（xB-xA）+2=3+xB，
由抛物线y2=4x及圆（x-1）2+y2=4可得交点的横坐标为1
∴xB∈（1，3）
∴3+xB∈（4，6）
故答案为：（4，6）
∴△FAB的周长=|AF|+|AB|+|BF|=xA+1+（xB-xA）+2=3+xB，
由抛物线y2=4x及圆（x-1）2+y2=4可得交点的横坐标为1
∴xB∈（1，3）
∴3+xB∈（4，6）
故答案为：（4，6）
点评：本题考查抛物线的定义，考查抛物线与圆的位置关系，确定B点横坐标的范围是关键．
练习册系列答案
相关题目
（2012•黄浦区二模）如图，已知圆柱的轴截面ABB1A1是正方形，C是圆柱下底面弧AB的中点，C1是圆柱上底面弧A1B1的中点，那么异面直线AC1与BC所成角的正切值为