Question

（理科题）（本小题12分）

已知数列{a_n}是等差数列，a₂＝3，a₅＝6，数列{b_n}的前n项和是T_n，且T_n＋b_n＝1.

(1)求数列{a_n}的通项公式与前n项的和；

(2)求数列{b_n}的通项公式.

 

Answer 1

【答案】

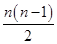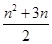(1)∴a_n＝2＋(n－1)＝n＋1.Sn＝na₁＋d＝. (2)证明：见解析。

【解析】

试题分析：（1）设{a_n}的公差为d，进而根据等差数列通项公式表示出a₂和a₅，求得a₁和d，则数列的通项公式和求和公式可得．

（2）根据T_n－T_n-1=b_n，整理得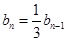，判断出{b_n}是等比数列．进而求得b₁，利用等比数列的通项公式求得答案．.

(1)设{a_n}的公差为d，则：a₂＝a₁＋d，a₅＝a₁＋4d.

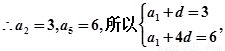   ……………2分

∴a₁＝2，d＝1    ……………3分

∴a_n＝2＋(n－1)＝n＋1.…………4分

Sn＝na₁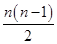＋d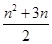＝.………………6分

(2)证明：当n＝1时，b₁＝T₁，

由T₁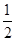＋b₁＝1，得b₁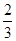＝. ………8分

当n≥2时，∵T_n＝1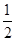－b_n，T_n－1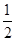＝1－b_n－1，

∴T_n－T_n－1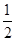＝ (b_n－1－b_n)，……………10分

即b_n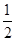＝ (b_n－1－b_n).

∴b_n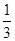＝b_n－1.  …………11分

∴{b_n}是以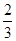为首项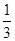，为公比的等比数列.∴b_n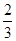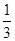＝·()^n－1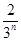＝.……………12分

考点：等差数列的通项公式；考查了等差数列的性质和等比数列的判定，等差数列的前n项和；等比数列的通项公式．

点评：先求出等差数列的前n项和S_n,然后就可以求出T_n,再利用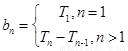可求{b_n}

的通项公式。