Question

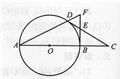如图，AB是⊙O的直径，延长AB到C，使BC=

1

2

AB，切线BF分别交切线CD及AD的延长线于E、F，求∠F的度数．

Answer 1

分析：由CD切⊙O于D，得OD⊥DC，而BC=

1

2

AB，则OC=2OD，得到∠C=60°，∠DOC=60°，得∠A=30°，由BF为⊙O的切线，得到BF⊥AB，利用互余即可求出∠F的度数．

解答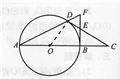：解：连接OD，如图，
∵CD切⊙O于D，
∴OD⊥DC，
又∵BC=

1

2

AB，
∴OC=2OD，
∴∠C=30°，∠DOC=60°，
而OD=OA，
∴∠A=30°，
又∵BF为⊙O的切线，
∴BF⊥AB，
∴∠F=90°-∠A=60°．

点评：本题考查了切线的性质：圆心与切点的连线垂直切线；过圆心垂直于切线的直线必过切点；过圆外一点引圆的两条切线，切线长相等．也考查了在直角三角形中一直角边等于斜边的一半，则这条直角所对的角为30度．