题目内容
已知变量x,y满足约束条件
,则z=2x•4y的最大值为( )
|
分析:先画出可行域,再把可行域的几个角点分别代入,看哪个角点对应的函数值最大即可.
解答:解:由于目标函数 z=2x•4y =2x+2y,令 m=x+2y,当m最大时,目标函数 z就最大.
画出可行域如图:可得点C(3,1)为最优解,m最大为5,故目标函数 z=2x•4y =2x+2y 的最大值为25=32,
故选B.

画出可行域如图:可得点C(3,1)为最优解,m最大为5,故目标函数 z=2x•4y =2x+2y 的最大值为25=32,
故选B.

点评:本题主要考查简单的线性规划问题,一般在求目标函数的最值时,常用角点法,就是求出可行域的几个角点,分别代入目标函数,即可求出目标函数的最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
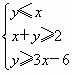 ,则目标函数Z=2x+y的最大值为________.
,则目标函数Z=2x+y的最大值为________. 则目标函数
则目标函数