题目内容
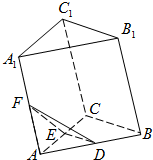（2013•江苏）如图，在三棱柱A1B1C1-ABC中，D，E，F分别是AB，AC，AA1的中点，设三棱锥F-ADE的体积为V1，三棱柱A1B1C1-ABC的体积为V2，则V1：V2=1：24
1：24
．分析：由三角形的相似比等于面积比的平方得到棱锥和棱柱的底面积的比值，由题意棱柱的高是棱锥的高的2倍，然后直接由体积公式可得比值．
解答：解：因为D，E，分别是AB，AC的中点，所以S△ADE：S△ABC=1：4，
又F是AA1的中点，所以A1到底面的距离H为F到底面距离h的2倍．
即三棱柱A1B1C1-ABC的高是三棱锥F-ADE高的2倍．
所以V1：V2=
=
=1：24．
故答案为1：24．
又F是AA1的中点，所以A1到底面的距离H为F到底面距离h的2倍．
即三棱柱A1B1C1-ABC的高是三棱锥F-ADE高的2倍．
所以V1：V2=
| ||
| S△ABC•H |
| 1 |
| 24 |
故答案为1：24．
点评：本题考查了棱柱和棱锥的体积公式，考查了相似多边形的面积的比等于相似比的平方，是基础的计算题．
练习册系列答案
相关题目
（2013•江苏）如图，游客从某旅游景区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C．现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50m/min．在甲出发2min后，乙从A乘缆车到B，在B处停留1min后，再从匀速步行到C．假设缆车匀速直线运动的速度为130m/min，山路AC长为1260m，经测量，cosA=
（2013•江苏）如图，在平面直角坐标系xOy中，点A（0，3），直线l：y=2x-4．设圆C的半径为1，圆心在l上．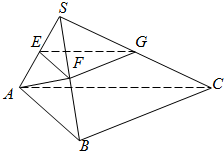
（2013•江苏）如图，在三棱锥S-ABC中，平面SAB⊥平面SBC，AB⊥BC，AS=AB，过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．求证：
（2013•江苏）如图是一个算法的流程图，则输出的n的值是