题目内容

已知定义在R上的单调函数f(x)，存在实数x0，使得对于任意实数x1，x2，总有f(x0x1+x0x2)=f(x0)+f(x1)+f(x2)恒成立．

(Ⅰ)求x0的值；

(Ⅱ)若f(x0)=1，且对任意正整数n，有an=,bn=f()+1，记Sn=a1a2+a2a3+…+anan+1，Tn=b1b2+b2b3+…+bnbn+1,比较Sn与Tn的大小关系，并给出证明．

解：(Ⅰ)令x1=x2=0得f(0)=f(x0)+2f(0)，

 ∴f(x0)=-f(0)．        ①

令x1=1，x2=0，得f(x0)=f(x0)+f(1)+f(0)，

∴f(1)=-f(0)．          ②

由①②得f(x0)=f(1)．

∵f(x)为单调函数，∴x0=1．

(Ⅱ)由(Ⅰ)得f(x1+x2)=f(x1)+f(x2)+f(1)=f(x1)+f(x2)+1，

∵f(n+1)=f(n)+f(1)+1=f(n)+2，f(1)=1，∴f(n)=2n-1．(n∈Z+)

∴an=.

又∵f（1）=f（+）=f（）+f（）+f（1）

∴f（）=0，b1=f（）+1.

又∵

∴2bn+1=2f()+2=f()+1=bn.

∴bn=()n-1.

∴Sn=

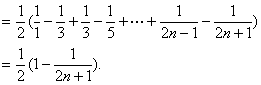
Tn=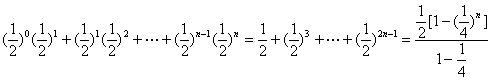

=

∴

∵4n=(3+1)n=3n+3n-1+…+3+≥3n+1＞2n+1,

∴

∴


练习册系列答案
相关题目
15、已知定义在R上的单调函数f（x）满足：存在实数x0，使得对于任意实数x1，x2，总有f（x0x1+x0x2）=f（x0）+f（x1）+f（x2）恒成立，则（i）f（1）+f（0）=
0
（ii）x0的值为
1
．
已知定义在R上的单调函数f（x），存在实数x0，使得对于任意实数x1，x2总有f（x0x1+x0x2）=f（x0）+f（x1）+f（x2）恒成立
（1）求x0的值；
（2）若f（x0）=1，且对任意正整数n，有an=
1
f(n)
，bn=f(
1
2n
)+1，记Sn=a1a2+a2a3+…+anan+1，Tn=b1b2+b2b3+…+bnbn+1，求Sn和Tn；
（3）若不等式an+1+an+2+…+a2n＞
4
35
[log
1
2
(x+1)-log
1
2
(9x2-1)+1]对任意不小于2的正整数n都成立，求x的取值范围．
已知定义在R上的单调函数y=f（x），当x＜0时，f（x）＞1，且对任意的实数x，y∈R，有f（x+y）=f（x）f（y），
（1）求f（0），并写出适合条件的函数f（x）的一个解析式；
（2）数列{an}满足a1=f(0)且f(an+1)=
1
f(-2-an)
(n∈N+)，
①求通项公式an的表达式；
②令bn=(
1
2
)an，Sn=b1+b2+…+bn，Tn=
1
a1a2
+
1
a2a3
+…+
1
anan+1
，试比较Sn与
4
3
Tn的大小，并加以证明；
③当a＞1时，不等式
1
an+1
+
1
an+2
+…+
1
a2n
＞
12
35
(log a+1x-log ax+1)对于不小于2的正整数n恒成立，求x的取值范围．
（2009•黄冈模拟）已知定义在R上的单调函数f（x），存在实数x0，使得对于任意实数x1，x2，总有f（x0x1+x0x2）=f（x0）+f（x1）+f（x2）恒成立．
（1）求x0的值；
（2）若f（x0）=1，且对于任意正整数n，有an=
1
f(n)
，bn=f(
1
2n
)+1，记Sn=a1a2+a2a3+…+anan+1，Tn=b1b2+b2b3+…+bnbn+1，比较
4
3
Sn与Tn的大小关系，并给出证明；
（3）在（2）的条件下，若不等式an+1+an+2+…+a2n＞
4
35
[log
1
2
(x+1)-log
1
2
(9x2-1)+1]对任意不小于2的正整数n都成立，求x的取值范围．
（2013•广州三模）已知定义在R上的单调函数f（x），存在实数x0使得对任意实数x1，x2，总有f（x0x1+x0x2）=f（x0）+f（x1）+f（x2）恒成立．
（1）求x0的值；
（2）若f（x0）=1，且对任意的正整数n．有an=
1
f(n)
，bn=f(
1
2n
)+1，记Sn=a1a2+a2a3+…+anan+1，Tn=b1b2+b2b3+…+bnbn+1，比较
4
3
Sn与Tn的大小关系，并给出证明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网