题目内容
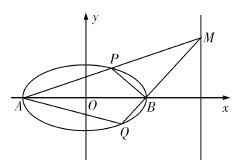
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
, ![]() 为过定点
为过定点![]() 的两条直线.
的两条直线.
(1)若![]() 与抛物线
与抛物线![]() 均无交点,且
均无交点,且![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的取值范围;
的取值范围;
(2)若![]() 与抛物线
与抛物线![]() 交于两个不同的点
交于两个不同的点![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 过点
过点![]() ,求圆
,求圆![]() 的方程.
的方程.
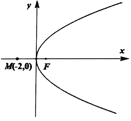
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】试题分析:(1) 设直线![]() 的方程为
的方程为![]() ,代入抛物线得
,代入抛物线得![]()
即![]() ,由于
,由于![]() 与抛物线
与抛物线![]() 无交点所以
无交点所以![]()
同理![]() 与抛物线
与抛物线![]() 均无交点,然后取交集即可;(2) 由①得
均无交点,然后取交集即可;(2) 由①得![]() ,
, ![]() ,由于
,由于![]() ,所以
,所以![]() ,计算得
,计算得![]() ,此时圆心
,此时圆心![]() ,满足
,满足
 ,从而得到圆
,从而得到圆![]() 的方程.
的方程.
试题解析:
(1)当![]() 的斜率不存在时,
的斜率不存在时, ![]() 的斜率为0,显然不符合题意.
的斜率为0,显然不符合题意.
所以设直线![]() 的方程为
的方程为![]() ,代入抛物线得
,代入抛物线得![]()
即![]() ………①
………①
由于![]() 与抛物线
与抛物线![]() 无交点所以
无交点所以![]()
即有![]() ,∴
,∴![]() ………②
………②
同理, ![]() 方程为
方程为![]() ,
,
由![]() 与抛物线
与抛物线![]() 无交点可得
无交点可得![]() ,
,
即![]() ………③
………③
由②③得![]() ,得
,得![]() 或
或![]()
(2)设![]() ,由①得
,由①得
![]() ,
, ![]() ,
,
所以![]() 易得
易得![]() ,
, ![]()
由于![]() ,所以
,所以![]() ,而
,而![]()
即![]() ,即
,即![]()
即 ,得
,得![]() ,
,
此时圆心![]() ,则
,则
 ,
,
半径
所求的圆方程为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目