题目内容
设a为实数, 函数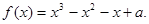
(Ⅰ)求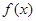 的极值.
的极值.
(Ⅱ)当a在什么范围内取值时,曲线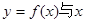 轴仅有一个交点.
轴仅有一个交点.
【答案】
(Ⅰ) 极大值是 ,极小值是
,极小值是 ;(Ⅱ)
;(Ⅱ)  ∪(1,+∞)。
∪(1,+∞)。
【解析】
试题分析:(I) =3
=3 -2
-2 -1若
-1若 =0,则
=0,则 ==-
==- ,
, =1
=1
当 变化时,
变化时, ,
, 变化情况如下表:
变化情况如下表:
|
|
(-∞,- |
- |
(- |
1 |
(1,+∞) |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
∴ 的极大值是
的极大值是 ,极小值是
,极小值是 --------8分
--------8分
(II)由(I)可知,取足够大的正数时,有 >0,取足够小的负数时有
>0,取足够小的负数时有 <0,
<0,
结合 的单调性可知:
的单调性可知:
 <0,或
<0,或 -1>0时,曲线
-1>0时,曲线 =
= 与
与 轴仅有一个交点,
轴仅有一个交点,
∴当 ∪(1,+∞)时,曲线
∪(1,+∞)时,曲线 =
= 与
与 轴仅有一个交点。 14分
轴仅有一个交点。 14分
考点:利用导数研究函数的极值;利用导数研究函数的单调性。
点评:做此题的关键是分析出:要满足题意只需极大值小于0或者极小值大于0.考查了学生分析问题,解决问题的能力。属于中档题型。

练习册系列答案
相关题目

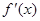 ,且
,且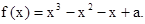
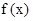 的极值及单调区间;
的极值及单调区间;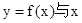 轴仅有一个交点?[来源:学§
轴仅有一个交点?[来源:学§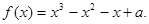
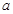 在什么范围内取值时,曲线y= f(x)与x轴仅有一个交点。
在什么范围内取值时,曲线y= f(x)与x轴仅有一个交点。