Question

【选修4—1：几何证明选讲】

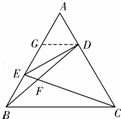
 如图，在正△ABC中，点D,E分别在边AC, AB上，且AD=AC

AE=AB，BD，CE相交于点F.

 （1）求证：A，E，F，D四点共圆；

 （2）若正△ABC的边长为2，求A，E，F，D所在圆的半径．

Answer 1

　

．	（Ⅰ）证明：∵AE=AB， ∴BE=AB， ∵在正△ABC中，AD=AC， ∴AD=BE， 又∵AB=BC，∠BAD=∠CBE， ∴△BAD≌△CBE， ∴∠ADB=∠BEC， 即∠ADF+∠AEF=π，所以A，E，F，D四点共圆．…（5分） （Ⅱ）解：如图， 取AE的中点G，连接GD，则AG=GE=AE， ∵AE=AB， ∴AG=GE=AB=， ∵AD=AC=，∠DAE=60°， ∴△AGD为正三角形， ∴GD=AG=AD=，即GA=GE=GD=， 所以点G是△AED外接圆的圆心，且圆G的半径为． 由于A，E，F，D四点共圆，即A，E，F，D四点共圆G，其半径为．…（10分）