题目内容
A、B是非空集合，定义A×B={x|x∈A∪B，且x∉A∩B}，若A={x|y=| x2-3x |
分析：集合A为函数y=
的定义域，只要x2-3x≥0，解出x的范围；集合B为函数y=3x的值域（0，+∞），由A×B定义求出A∪B和A∩B，再求A×B即可．
| x2-3x |
解答：解：A={x|y=
}=x|x2-3x≥0=x|x≤0或x≥3，
B={y|y=3x}={y|y＞0}，
所以A∪B=R，A∩B=[3，+∞），
故A×B=（-∞，3）．
故答案为：（-∞，3）
| x2-3x |
B={y|y=3x}={y|y＞0}，
所以A∪B=R，A∩B=[3，+∞），
故A×B=（-∞，3）．
故答案为：（-∞，3）
点评：本题考查集合的表示和集合的交集、并集和补集运算，解题的关键是理解好A×B的定义．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
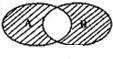如图所示的韦恩图中，A、B是非空集合，定义A*B表示阴影部分的集合．若x，y∈R，A={x|y=
（2013•牡丹江一模）如图所示的韦恩图中，A、B是非空集合，定义A*B表示阴影部分集合．若x，y∈R，