题目内容
已知a＞0，函数f（x）=lnx﹣ax2，x＞0．
（Ⅰ）求f（x）的单调区间；
（Ⅱ）若存在均属于区间[1，3]的α，β，且β﹣α≥1，使f（α）=f（β）证明：
．
（Ⅰ）求f（x）的单调区间；
（Ⅱ）若存在均属于区间[1，3]的α，β，且β﹣α≥1，使f（α）=f（β）证明：
．（I）解：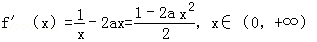
，
令f′（x）=0，解得x=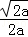
，
当x变化时，f'（x），f（x）的变化情况如下表：
所以，f（x）的单调递增区间是 
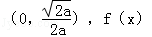的单调递减区间是 
．
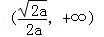（II）证明：由f（α）=f（β）及（I）的结论知 ，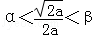
从而f（x）在[α，β]上的最小值为f（a）．
又由β﹣α≥1，α，β∈[1，3]，
知1≤α≤2≤β≤3．
故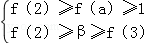
，即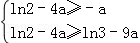 
从而，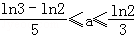
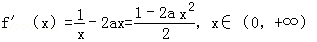，令f′（x）=0，解得x=
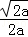，当x变化时，f'（x），f（x）的变化情况如下表：
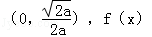的单调递减区间是 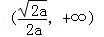．（II）证明：由f（α）=f（β）及（I）的结论知 ，
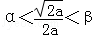
从而f（x）在[α，β]上的最小值为f（a）．
又由β﹣α≥1，α，β∈[1，3]，
知1≤α≤2≤β≤3．
故
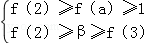，即 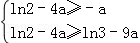从而，
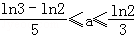
练习册系列答案
相关题目
已知a＞0，函数f（x）=ax2+bx+c，若x0满足关于x的方程2ax+b=0，则下列选项的命题中为假命题的是（ ）
| A、?x∈R，f（x）≤f（x0） | B、?x∈R，f（x）≥f（x0） | C、?x∈R，f（x）≤f（x0） | D、?x∈R，f（x）≥f（x0） |